UP | HOME

List of filters - Matlab Implementation

Table of Contents

1 Low Pass

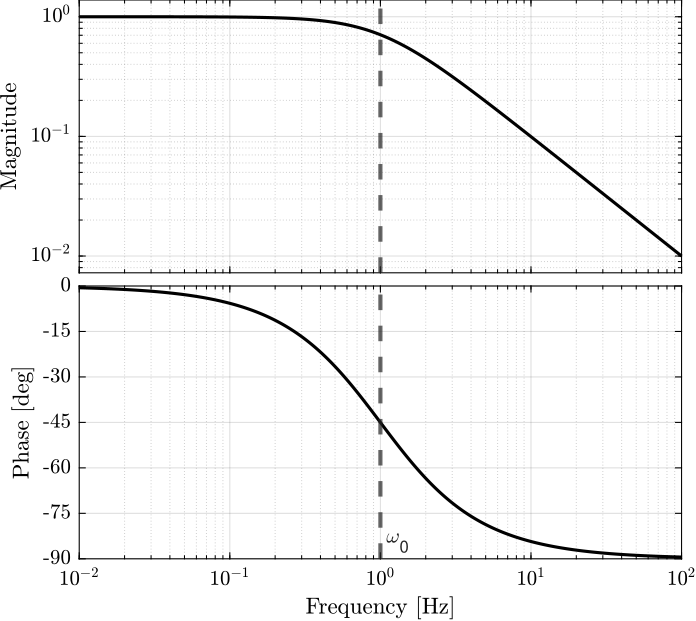
1.1 First Order Low Pass Filter

\[ H(s) = \frac{1}{1 + s/\omega_0} \]

Parameters:

  • \(\omega_0\): cut-off frequency in [rad/s]

Characteristics:

  • Low frequency gain of \(1\)
  • Roll-off equals to -20 dB/dec

Matlab code: 

w0 = 2*pi; % Cut-off Frequency [rad/s]

H = 1/(1 + s/w0);

filter_low_pass_first_order.png

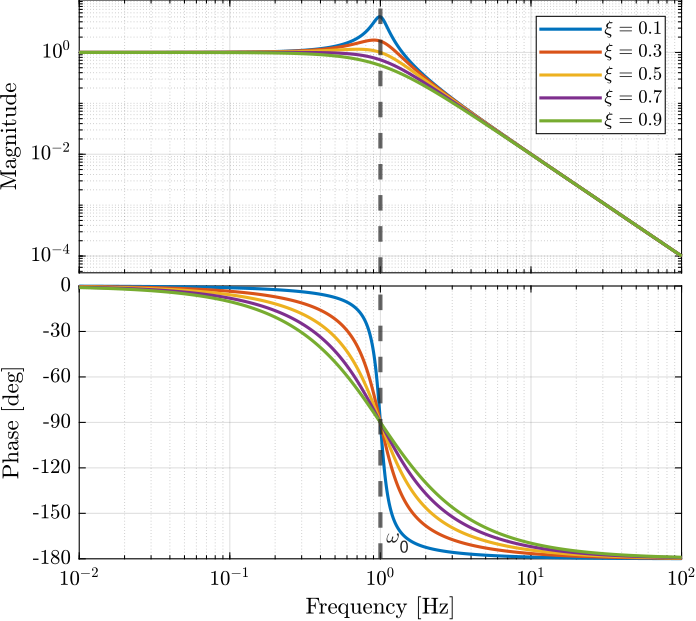
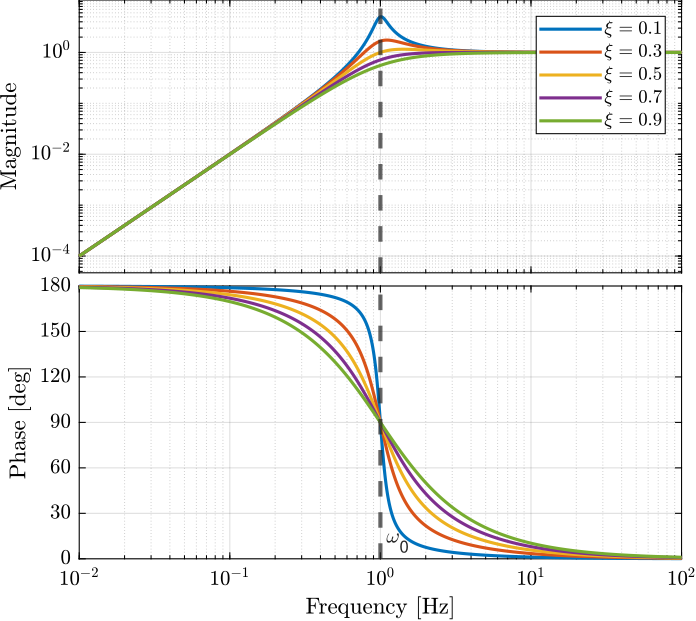
1.2 Second Order

\[ H(s) = \frac{1}{1 + 2 \xi / \omega_0 s + s^2/\omega_0^2} \]

Parameters:

  • \(\omega_0\):
  • \(\xi\): Damping ratio

Characteristics:

  • Low frequency gain: 1
  • High frequency roll off: - 40 dB/dec

Matlab code: 

w0 = 2*pi; % Cut-off frequency [rad/s]
xi = 0.3; % Damping Ratio

H = 1/(1 + 2*xi/w0*s + s^2/w0^2);

filter_low_pass_second_order.png

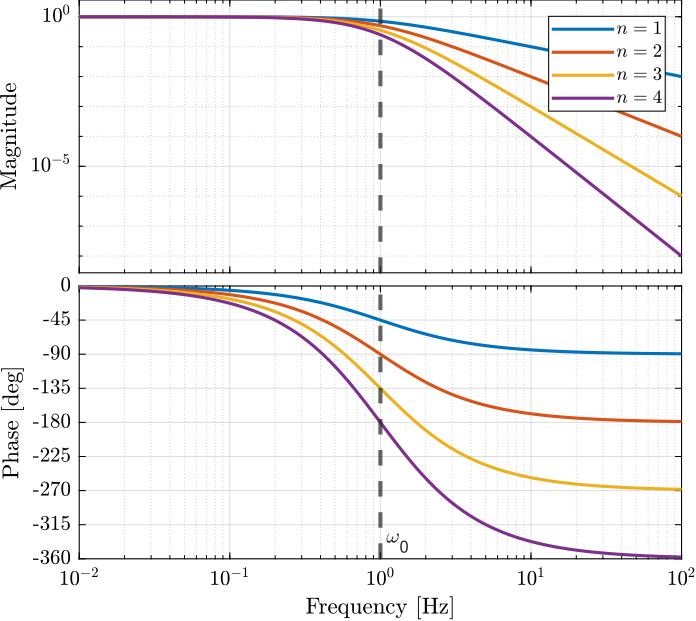
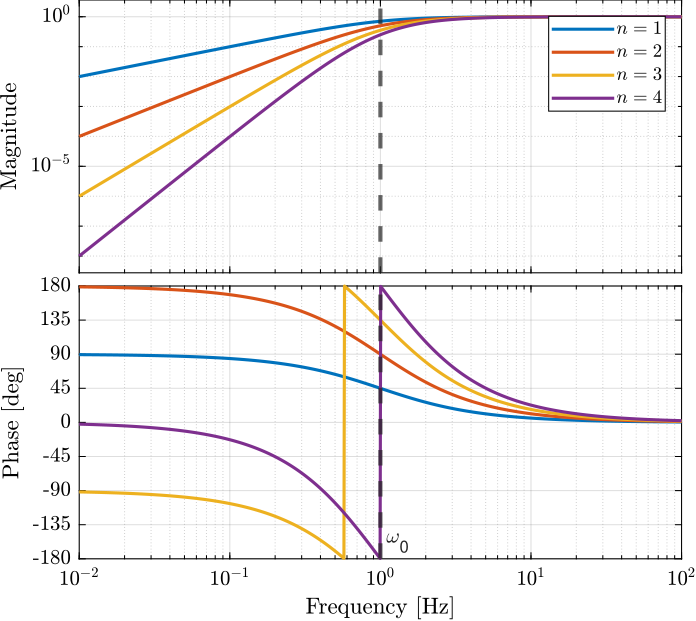
1.3 Combine multiple first order filters

\[ H(s) = \left( \frac{1}{1 + s/\omega_0} \right)^n \]

Matlab code: 

w0 = 2*pi; % Cut-off frequency [rad/s]
n = 3; % Filter order

H = (1/(1 + s/w0))^n;

filter_low_pass_first_order_add.png

2 High Pass

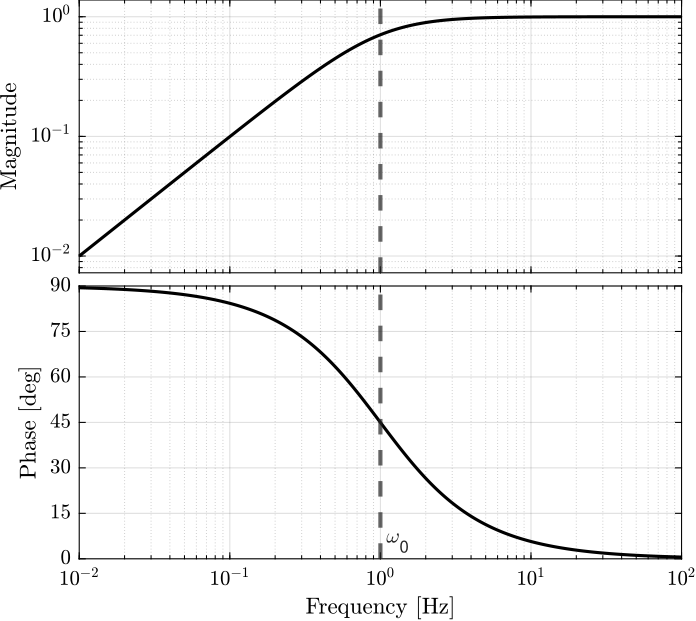
2.1 First Order

\[ H(s) = \frac{s/\omega_0}{1 + s/\omega_0} \]

Parameters:

  • \(\omega_0\): cut-off frequency in [rad/s]

Characteristics:

  • High frequency gain of \(1\)
  • Low frequency slow of +20 dB/dec

Matlab code: 

w0 = 2*pi; % Cut-off frequency [rad/s]

H = (s/w0)/(1 + s/w0);

filter_high_pass_first_order.png

2.2 Second Order

\[ H(s) = \frac{s^2/\omega_0^2}{1 + 2 \xi / \omega_0 s + s^2/\omega_0^2} \]

Parameters:

  • \(\omega_0\):
  • \(\xi\): Damping ratio

Matlab code: 

w0 = 2*pi; % [rad/s]
xi = 0.3;

H = (s^2/w0^2)/(1 + 2*xi/w0*s + s^2/w0^2);

filter_high_pass_second_order.png

2.3 Combine multiple filters

\[ H(s) = \left( \frac{s/\omega_0}{1 + s/\omega_0} \right)^n \]

Matlab code: 

w0 = 2*pi; % [rad/s]
n = 3;

H = ((s/w0)/(1 + s/w0))^n;

filter_high_pass_first_order_add.png

3 Band Pass

3.1 Second Order

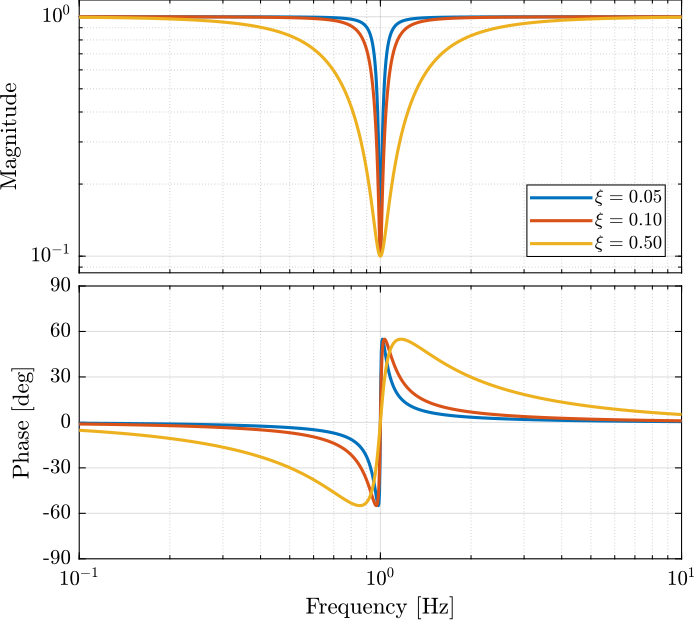
4 Notch

4.1 Second Order

\begin{equation} \frac{s^2 + 2 g_c \xi \omega_n s + \omega_n^2}{s^2 + 2 \xi \omega_n s + \omega_n^2} \end{equation}

Parameters:

  • \(\omega_n\): frequency of the notch
  • \(g_c\): gain at the notch frequency
  • \(\xi\): damping ratio (notch width)

Matlab code: 

gc = 0.02;
xi = 0.1;
wn = 2*pi;

H = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

filter_notch_xi.png

filter_notch_gc.png

5 Chebyshev

5.1 Chebyshev Type I

n = 4; % Order of the filter
Rp = 3; % Maximum peak-to-peak ripple [dB]
Wp = 2*pi; % passband-edge frequency [rad/s]

[A,B,C,D] = cheby1(n, Rp, Wp, 'high', 's');
H = ss(A, B, C, D);

6 Lead - Lag

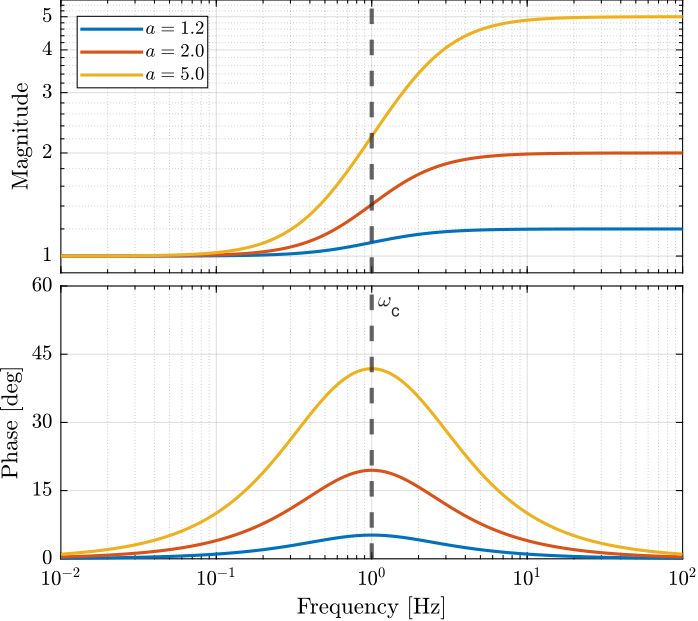
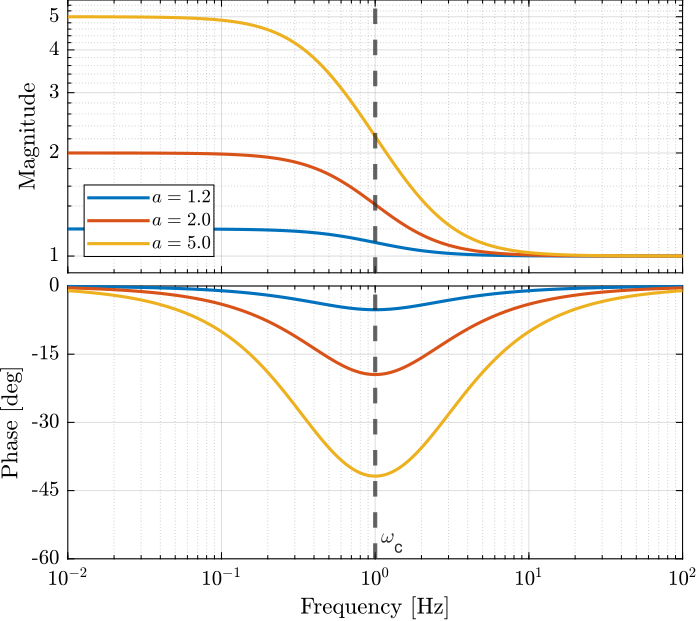
6.1 Lead

\begin{equation} H(s) = \frac{1 + \frac{s}{w_c/\sqrt{a}}}{1 + \frac{s}{w_c \sqrt{a}}}, \quad a > 1 \end{equation}

Parameters:

  • \(\omega_c\): frequency at which the phase lead is maximum
  • \(a\): parameter to adjust the phase lead, also impacts the high frequency gain

Characteristics:

  • the low frequency gain is \(1\)
  • the high frequency gain is \(a\)
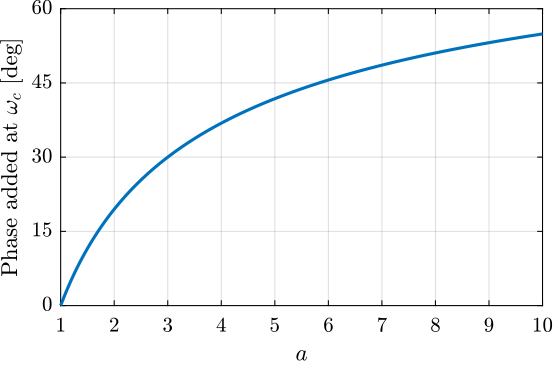
  • the phase lead at \(\omega_c\) is equal to (Figure 10): \[ \angle H(j\omega_c) = \tan^{-1}(\sqrt{a}) - \tan^{-1}(1/\sqrt{a}) \]

Matlab code: 

a  = 0.6;  % Amount of phase lead / width of the phase lead / high frequency gain
wc = 2*pi; % Frequency with the maximum phase lead [rad/s]

H = (1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));

filter_lead.png

filter_lead_effect_a_phase.png

6.2 Lag

\begin{equation} H(s) = \frac{w_c \sqrt{a} + s}{\frac{w_c}{\sqrt{a}} + s}, \quad a > 1 \end{equation}

Parameters:

  • \(\omega_c\): frequency at which the phase lag is maximum
  • \(a\): parameter to adjust the phase lag, also impacts the low frequency gain

Characteristics:

  • the low frequency gain is increased by a factor \(a\)
  • the high frequency gain is \(1\) (unchanged)
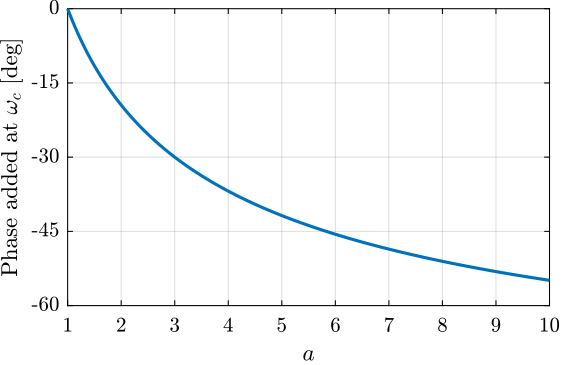
  • the phase lag at \(\omega_c\) is equal to (Figure 12): \[ \angle H(j\omega_c) = \tan^{-1}(1/\sqrt{a}) - \tan^{-1}(\sqrt{a}) \]

Matlab code: 

a  = 0.6;  % Amount of phase lag / width of the phase lag / high frequency gain
wc = 2*pi; % Frequency with the maximum phase lag [rad/s]

H = (wc*sqrt(a) + s)/(wc/sqrt(a) + s);

filter_lag.png

filter_lag_effect_a_phase.png

7 Complementary

8 Performance Weight

8.1 Nice combination

\begin{equation} W(s) = G_c * \left(\frac{\frac{1}{\omega_0}\sqrt{\frac{1 - \left(\frac{G_0}{G_c}\right)^{\frac{2}{n}}}{1 - \left(\frac{G_c}{G_\infty}\right)^{\frac{2}{n}}}} s + \left(\frac{G_0}{G_c}\right)^{\frac{1}{n}}}{\frac{1}{\omega_0} \sqrt{\frac{1 - \left(\frac{G_0}{G_c}\right)^{\frac{2}{n}}}{\left(\frac{G_\infty}{G_c}\right)^{\frac{2}{n}} - 1}} s + 1}\right)^n \end{equation} 
n = 2; w0 = 2*pi*11; G0 = 1/10; G1 = 1000; Gc = 1/2;
wL = Gc*(((G1/Gc)^(1/n)/w0*sqrt((1-(G0/Gc)^(2/n))/((G1/Gc)^(2/n)-1))*s + (G0/Gc)^(1/n))/(1/w0*sqrt((1-(G0/Gc)^(2/n))/((G1/Gc)^(2/n)-1))*s + 1))^n;

n = 3; w0 = 2*pi*9; G0 = 10000; G1 = 0.1; Gc = 1/2;
wH = Gc*(((G1/Gc)^(1/n)/w0*sqrt((1-(G0/Gc)^(2/n))/((G1/Gc)^(2/n)-1))*s + (G0/Gc)^(1/n))/(1/w0*sqrt((1-(G0/Gc)^(2/n))/((G1/Gc)^(2/n)-1))*s + 1))^n;

8.2 Alternative

w0 = 2*pi; % [rad/s]
A = 1e-2;
M = 5;

H = (s/sqrt(M) + w0)^2/(s + w0*sqrt(A))^2;

weight_first_order.png

9 Combine Filters

9.1 Additive

  • [ ] Explain how phase and magnitude combine

9.2 Multiplicative

10 Filters representing noise

Let’s consider a noise \(n\) that is shaped from a white-noise \(\tilde{n}\) with unitary PSD (\(\Phi_\tilde{n}(\omega) = 1\)) using a transfer function \(G(s)\). The PSD of \(n\) is then: \[ \Phi_n(\omega) = |G(j\omega)|^2 \Phi_{\tilde{n}}(\omega) = |G(j\omega)|^2 \]

The PSD \(\Phi_n(\omega)\) is expressed in \(\text{unit}^2/\text{Hz}\).

And the root mean square (RMS) of \(n(t)\) is: \[ \sigma_n = \sqrt{\int_{0}^{\infty} \Phi_n(\omega) d\omega} \]

10.1 First Order Low Pass Filter

\[ G(s) = \frac{g_0}{1 + \frac{s}{\omega_c}} \] 

g0 = 1; % Noise Density in unit/sqrt(Hz)
wc = 1; % Cut-Off frequency [rad/s]

G = g0/(1 + s/wc);

% Frequency vector [Hz]
freqs = logspace(-3, 3, 1000);

% PSD of n in [unit^2/Hz]
Phi_n = abs(squeeze(freqresp(G, freqs, 'Hz'))).^2;

% RMS value of n in [unit, rms]
sigma_n = sqrt(trapz(freqs, Phi_n))

\[ \sigma = \frac{1}{2} g_0 \sqrt{\omega_c} \] with:

  • \(g_0\) the Noise Density of \(n\) in \(\text{unit}/\sqrt{Hz}\)
  • \(\omega_c\) the bandwidth over which the noise is located, in rad/s
  • \(\sigma\) the rms noise

If the cut-off frequency is to be expressed in Hz: \[ \sigma = \frac{1}{2} g_0 \sqrt{2\pi f_c} = \sqrt{\frac{\pi}{2}} g_0 \sqrt{f_c} \]

Thus, if a sensor is said to have a RMS noise of \(\sigma = 10 nm\ rms\) over a bandwidth of \(\omega_c = 100 rad/s\), we can estimated the noise density of the sensor to be (supposing a first order low pass filter noise shape): \[ g_0 = \frac{2 \sigma}{\sqrt{\omega_c}} \quad \left[ m/\sqrt{Hz} \right] \] 

2*10e-9/sqrt(100)

2e-09

6*0.5*20e-12*sqrt(2*pi*100)

1.504e-09

Author: Dehaeze Thomas

Created: 2020-10-29 jeu. 10:09