UP | HOME

Encoder - Test Bench

Table of Contents

1 Experimental Setup

The experimental Setup is schematically represented in Figure 1.

The mass can be vertically moved using the amplified piezoelectric actuator. The displacement of the mass (relative to the mechanical frame) is measured both by the interferometer and by the encoder.

exp_setup_schematic.png

Figure 1: Schematic of the Experiment

IMG_20201023_153905.jpg

Figure 2: Side View of the encoder

IMG_20201023_153914.jpg

Figure 3: Front View of the encoder

2 Huddle Test

The goal in this section is the estimate the noise of both the encoder and the intereferometer.

Nothing is then to the actuator such that the relative motion between the mass and the frame is as small as possible. Ideally, a mechanical part would clamp the two together, we here suppose that the APA is still enough to clamp the two together.

2.1 Load Data

load('mat/int_enc_huddle_test.mat', 'interferometer', 'encoder', 't');

interferometer = detrend(interferometer, 0);
encoder = detrend(encoder, 0);

2.2 Time Domain Results

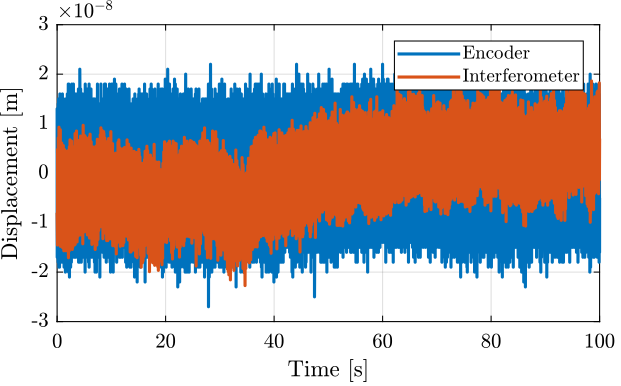
huddle_test_time_domain.png

Figure 4: Huddle test - Time domain signals

G_lpf = 1/(1 + s/2/pi/10);

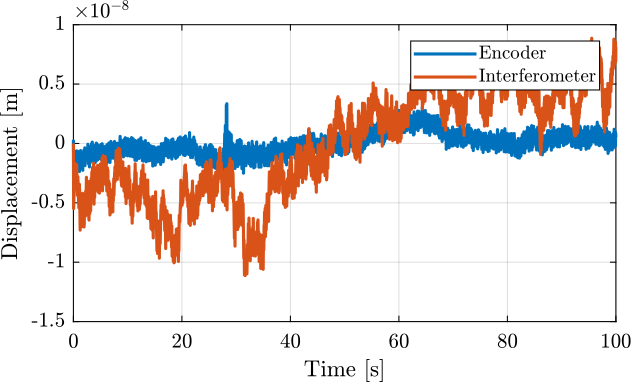
huddle_test_time_domain_filtered.png

Figure 5: Huddle test - Time domain signals filtered with a LPF at 10Hz

2.3 Frequency Domain Noise

Ts = 1e-4;
win = hann(ceil(10/Ts));

[p_i, f] = pwelch(interferometer, win, [], [], 1/Ts);
[p_e, ~] = pwelch(encoder,        win, [], [], 1/Ts);

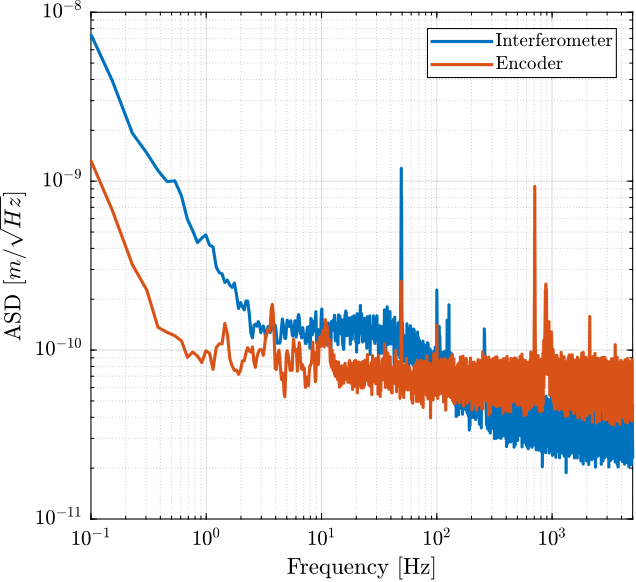
huddle_test_asd.png

Figure 6: Amplitude Spectral Density of the signals during the Huddle test

3 Comparison Interferometer / Encoder

The goal here is to make sure that the interferometer and encoder measurements are coherent. We may see non-linearity in the interferometric measurement.

3.1 Load Data

load('mat/int_enc_comp.mat', 'interferometer', 'encoder', 'u', 't');

interferometer = detrend(interferometer, 0);
encoder = detrend(encoder, 0);
u = detrend(u, 0);

3.2 Time Domain Results

int_enc_one_cycle.png

Figure 7: One cycle measurement

int_enc_one_cycle_error.png

Figure 8: Difference between the Encoder and the interferometer during one cycle

3.3 Difference between Encoder and Interferometer as a function of time

Ts = 1e-4;
d_i_mean = reshape(interferometer, [2/Ts floor(Ts/2*length(interferometer))]);
d_e_mean = reshape(encoder,        [2/Ts floor(Ts/2*length(encoder))]);

w0 = 2*pi*5; % [rad/s]
xi = 0.7;

G_lpf = 1/(1 + 2*xi/w0*s + s^2/w0^2);

d_err_mean = reshape(lsim(G_lpf, encoder - interferometer, t), [2/Ts floor(Ts/2*length(encoder))]);
d_err_mean = d_err_mean - mean(d_err_mean);

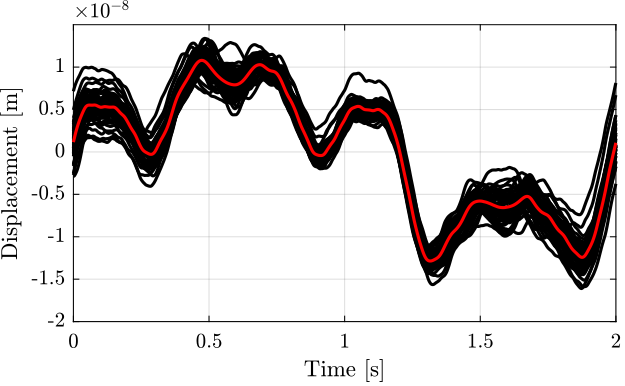
int_enc_error_mean_time.png

Figure 9: Difference between the two measurement in the time domain, averaged for all the cycles

3.4 Difference between Encoder and Interferometer as a function of position

Compute the mean of the interferometer measurement corresponding to each of the encoder measurement. 

[e_sorted, ~, e_ind] = unique(encoder);

i_mean = zeros(length(e_sorted), 1);
for i = 1:length(e_sorted)
  i_mean(i) = mean(interferometer(e_ind == i));
end

i_mean_error = (i_mean - e_sorted);

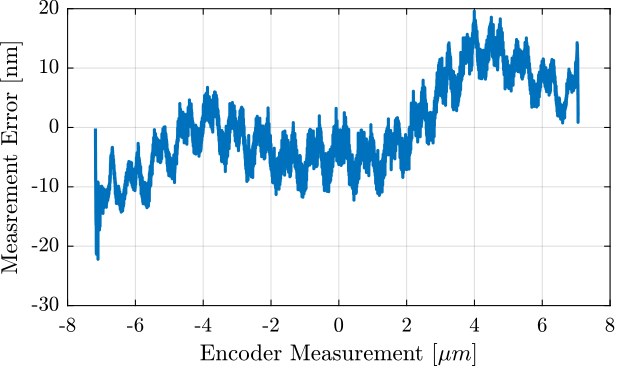
int_enc_error_mean_position.png

Figure 10: Difference between the two measurement as a function of the measured position by the encoder, averaged for all the cycles

The period of the non-linearity seems to be \(1.53 \mu m\) which corresponds to the wavelength of the Laser. 

win_length = 1530; % length of the windows (corresponds to 1.53 um)
num_avg = floor(length(e_sorted)/win_length); % number of averaging

i_init = ceil((length(e_sorted) - win_length*num_avg)/2); % does not start at the extremity

e_sorted_mean_over_period = mean(reshape(i_mean_error(i_init:i_init+win_length*num_avg-1), [win_length num_avg]), 2);

int_non_linearity_period_wavelength.png

Figure 11: Non-Linearity of the Interferometer over the period of the wavelength

4 Identification

4.1 Load Data

load('mat/int_enc_id_noise_bis.mat', 'interferometer', 'encoder', 'u', 't');

interferometer = detrend(interferometer, 0);
encoder = detrend(encoder, 0);
u = detrend(u, 0);

4.2 Identification

Ts = 1e-4; % Sampling Time [s]
win = hann(ceil(10/Ts));

[tf_i_est, f] = tfestimate(u, interferometer, win, [], [], 1/Ts);
[co_i_est, ~] = mscohere(u, interferometer, win, [], [], 1/Ts);

[tf_e_est, ~] = tfestimate(u, encoder, win, [], [], 1/Ts);
[co_e_est, ~] = mscohere(u, encoder, win, [], [], 1/Ts);

identification_dynamics_coherence.png

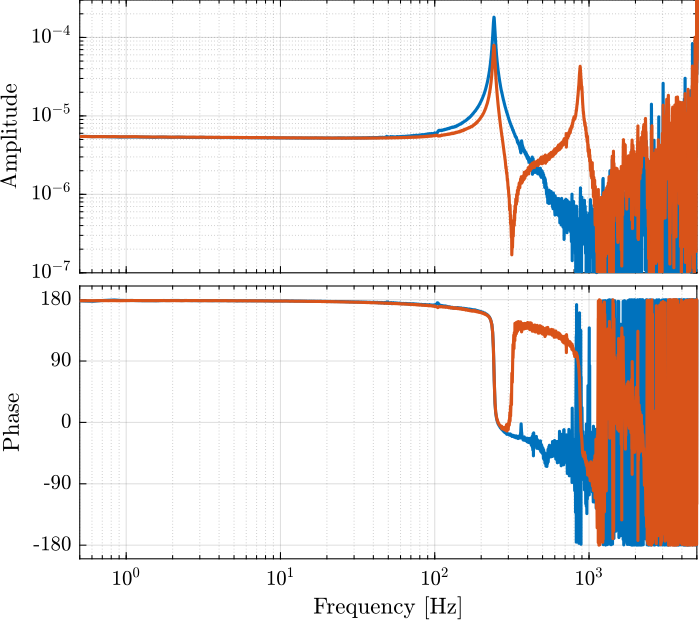
identification_dynamics_bode.png

5 Change of Stiffness due to Sensors stack being open/closed circuit

5.1 Load Data

oc = load('./mat/identification_open_circuit.mat', 't', 'encoder', 'u');
sc = load('./mat/identification_short_circuit.mat', 't', 'encoder', 'u');

5.2 Transfer Functions

Ts = 1e-4; % Sampling Time [s]
win = hann(ceil(10/Ts));

[tf_oc_est, f] = tfestimate(oc.u, oc.encoder, win, [], [], 1/Ts);
[co_oc_est, ~] = mscohere(  oc.u, oc.encoder, win, [], [], 1/Ts);

[tf_sc_est, ~] = tfestimate(sc.u, sc.encoder, win, [], [], 1/Ts);
[co_sc_est, ~] = mscohere(  sc.u, sc.encoder, win, [], [], 1/Ts);

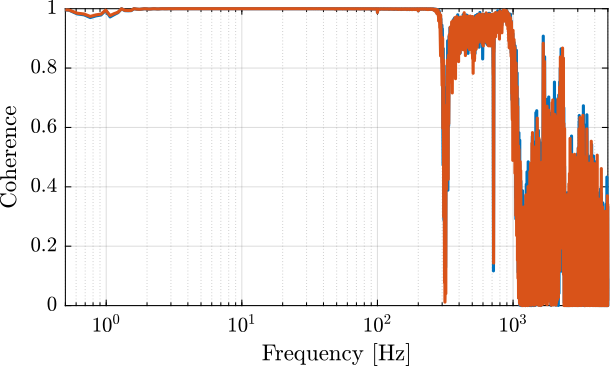
stiffness_force_sensor_coherence.png

stiffness_force_sensor_bode.png

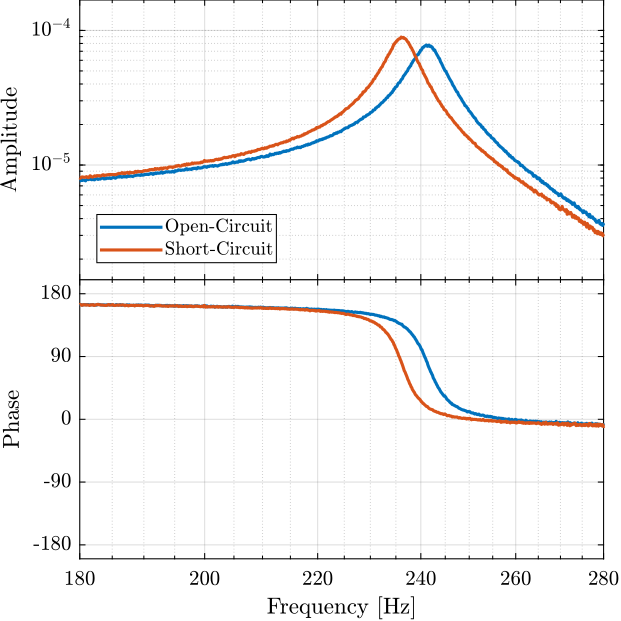
stiffness_force_sensor_bode_zoom.png

Figure 16: Zoom on the change of resonance

The change of resonance frequency / stiffness is very small and is not important here.

6 Generated Number of Charge / Voltage

Two stacks are used as actuator (in parallel) and one stack is used as sensor.

The amplifier gain is 20V/V (Cedrat LA75B).

6.1 Steps

load('./mat/force_sensor_steps.mat', 't', 'encoder', 'u', 'v');

figure;
tiledlayout(2, 1, 'TileSpacing', 'None', 'Padding', 'None');
nexttile;
plot(t, v);
xlabel('Time [s]'); ylabel('Measured voltage [V]');
nexttile;
plot(t, u);
xlabel('Time [s]'); ylabel('Actuator Voltage [V]');

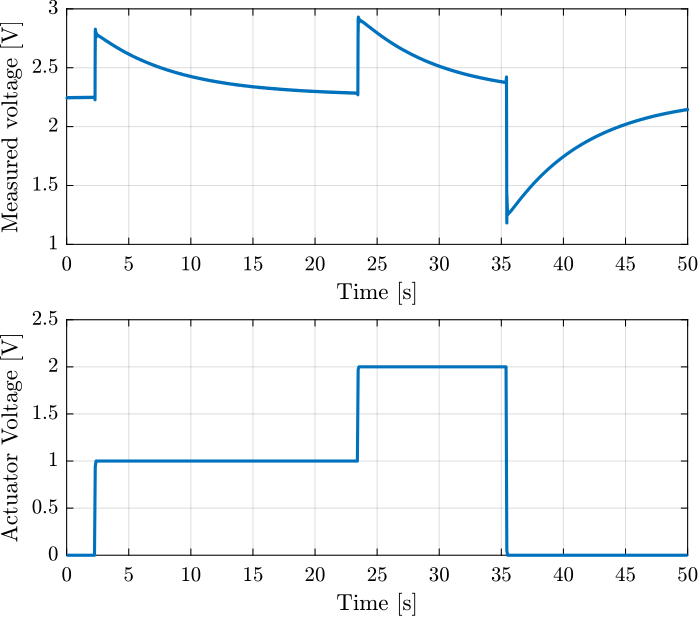
force_sen_steps_time_domain.png

Figure 17: Time domain signal during the 3 actuator voltage steps

Three steps are performed at the following time intervals: 

t_s = [ 2.5, 23;
       23.8, 35;
       35.8, 50];

Fit function: 

f = @(b,x) b(1).*exp(b(2).*x) + b(3);

We are interested by the b(2) term, which is the time constant of the exponential. 

tau = zeros(size(t_s, 1),1);
V0  = zeros(size(t_s, 1),1);

for t_i = 1:size(t_s, 1)
    t_cur = t(t_s(t_i, 1) < t & t < t_s(t_i, 2));
    t_cur = t_cur - t_cur(1);
    y_cur = v(t_s(t_i, 1) < t & t < t_s(t_i, 2));

    nrmrsd = @(b) norm(y_cur - f(b,t_cur)); % Residual Norm Cost Function
    B0 = [0.5, -0.15, 2.2];                        % Choose Appropriate Initial Estimates
    [B,rnrm] = fminsearch(nrmrsd, B0);     % Estimate Parameters ‘B’

    tau(t_i) = 1/B(2);
    V0(t_i)  = B(3);
end
\(tau\) [s] \(V_0\) [V]
6.47 2.26
6.76 2.26
6.49 2.25

With the capacitance being \(C = 4.4 \mu F\), the internal impedance of the Speedgoat ADC can be computed as follows: 

Cp = 4.4e-6; % [F]
Rin = abs(mean(tau))/Cp;

1494100.0

The input impedance of the Speedgoat’s ADC should then be close to \(1.5\,M\Omega\) (specified at \(1\,M\Omega\)).

How can we explain the voltage offset?

As shown in Figure 18 (taken from (Reza and Andrew 2006)), an input voltage offset is due to the input bias current \(i_n\).

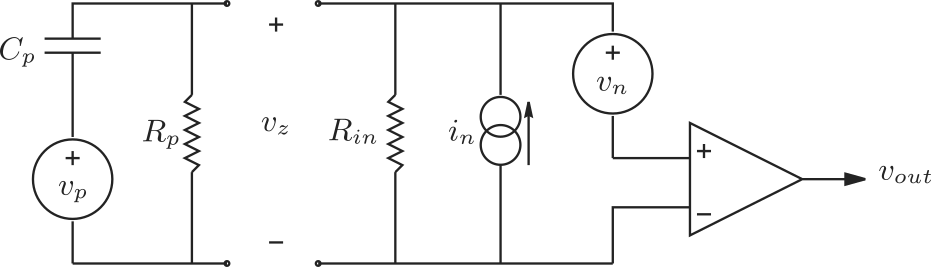
piezo_sensor_model_instrumentation.png

Figure 18: Model of a piezoelectric transducer (left) and instrumentation amplifier (right)

The estimated input bias current is then: 

in = mean(V0)/Rin;

1.5119e-06

An additional resistor in parallel with \(R_{in}\) would have two effects:

  • reduce the input voltage offset \[ V_{off} = \frac{R_a R_{in}}{R_a + R_{in}} i_n \]
  • increase the high pass corner frequency \(f_c\) \[ C_p \frac{R_{in}R_a}{R_{in} + R_a} = \tau_c = \frac{1}{f_c} \] \[ R_a = \frac{R_i}{f_c C_p R_i - 1} \]

If we allow the high pass corner frequency to be equals to 3Hz: 

fc = 3;
Ra = Rin/(fc*Cp*Rin - 1);

79804

With this parallel resistance value, the voltage offset would be: 

V_offset = Ra*Rin/(Ra + Rin) * in;

0.11454

Which is much more acceptable.

6.2 Add Parallel Resistor

A resistor of \(\approx 100\,k\Omega\) is added in parallel with the force sensor and the same kin. 

load('./mat/force_sensor_steps_R_82k7.mat', 't', 'encoder', 'u', 'v');

figure;
tiledlayout(2, 1, 'TileSpacing', 'None', 'Padding', 'None');
nexttile;
plot(t, v);
xlabel('Time [s]'); ylabel('Measured voltage [V]');
nexttile;
plot(t, u);
xlabel('Time [s]'); ylabel('Actuator Voltage [V]');

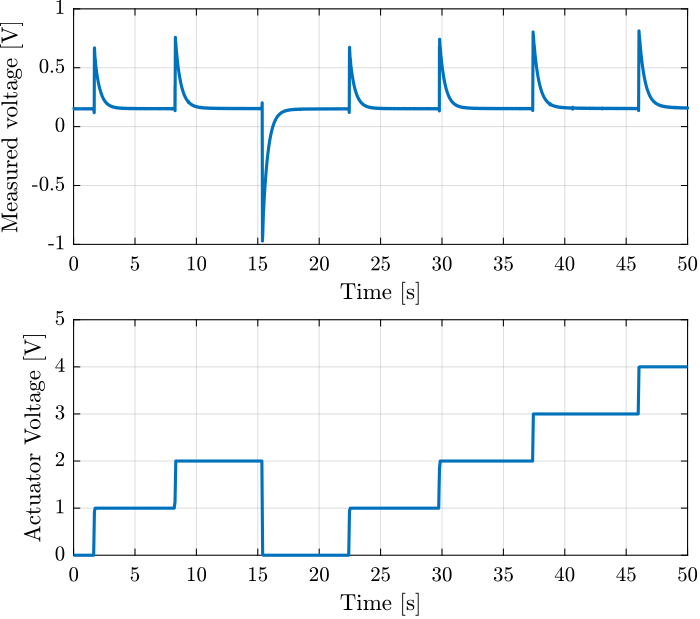
force_sen_steps_time_domain_par_R.png

Figure 19: Time domain signal during the actuator voltage steps

Three steps are performed at the following time intervals: 

t_s = [1.9,  6;
       8.5, 13;
      15.5, 21;
      22.6, 26;
      30.0, 36;
      37.5, 41;
      46.2, 49.5]

Fit function: 

f = @(b,x) b(1).*exp(b(2).*x) + b(3);

We are interested by the b(2) term, which is the time constant of the exponential. 

tau = zeros(size(t_s, 1),1);
V0  = zeros(size(t_s, 1),1);

for t_i = 1:size(t_s, 1)
    t_cur = t(t_s(t_i, 1) < t & t < t_s(t_i, 2));
    t_cur = t_cur - t_cur(1);
    y_cur = v(t_s(t_i, 1) < t & t < t_s(t_i, 2));

    nrmrsd = @(b) norm(y_cur - f(b,t_cur)); % Residual Norm Cost Function
    B0 = [0.5, -0.2, 0.2];                        % Choose Appropriate Initial Estimates
    [B,rnrm] = fminsearch(nrmrsd, B0);     % Estimate Parameters ‘B’

    tau(t_i) = 1/B(2);
    V0(t_i)  = B(3);
end

And indeed, we obtain a much smaller offset voltage and a much faster time constant.

\(tau\) [s] \(V_0\) [V]
0.43 0.15
0.45 0.16
0.43 0.15
0.43 0.15
0.45 0.15
0.46 0.16
0.48 0.16

Knowing the capacitance value, we can estimate the value of the added resistor (neglecting the input impedance of \(\approx 1\,M\Omega\)): 

Cp = 4.4e-6; % [F]
Rin = abs(mean(tau))/Cp;

101200.0

And we can verify that the bias current estimation stays the same: 

in = mean(V0)/Rin;

1.5305e-06

This validates the model of the ADC and the effectiveness of the added resistor.

6.3 Sinus

load('./mat/force_sensor_sin.mat', 't', 'encoder', 'u', 'v');

u       = u(t>25);
v       = v(t>25);
encoder = encoder(t>25) - mean(encoder(t>25));
t       = t(t>25);

The driving voltage is a sinus at 0.5Hz centered on 3V and with an amplitude of 3V (Figure 20).

force_sensor_sin_u.png

Figure 20: Driving Voltage

The full stroke as measured by the encoder is: 

max(encoder)-min(encoder)

5.005e-05

Its signal is shown in Figure 21.

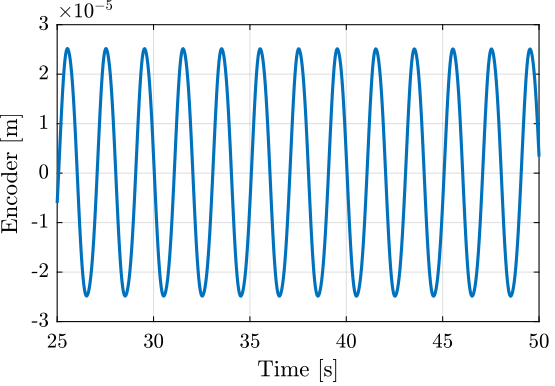
force_sensor_sin_encoder.png

Figure 21: Encoder measurement

The generated voltage by the stack is shown in Figure

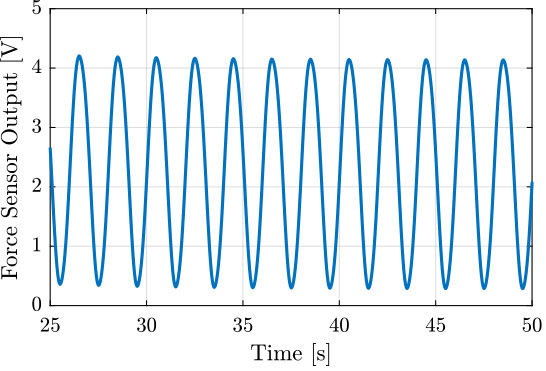
force_sensor_sin_stack.png

Figure 22: Voltage measured on the stack used as a sensor

The capacitance of the stack is 

Cp = 4.4e-6; % [F]

The corresponding generated charge is then shown in Figure 23.

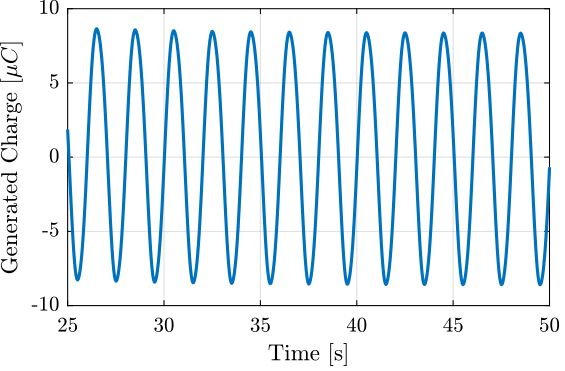
force_sensor_sin_charge.png

Figure 23: Generated Charge

The relation between the generated voltage and the measured displacement is almost linear as shown in Figure 24. 

b1 = encoder\(v-mean(v));

force_sensor_linear_relation.png

Figure 24: Almost linear relation between the relative displacement and the generated voltage

With a 16bits ADC, the resolution will then be equals to (in [nm]): 

abs((20/2^16)/(b1/1e9))

3.9838

Bibliography

Reza, Moheimani, and Fleming Andrew. 2006. Piezoelectric Transducers for Vibration Control and Damping. London: Springer.

Author: Dehaeze Thomas

Created: 2020-11-04 mer. 20:38