<?xml version="1.0" encoding="utf-8"?>
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN"
"http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd">
<html xmlns="http://www.w3.org/1999/xhtml" lang="en" xml:lang="en">
<head>
<!-- 2021-09-02 jeu. 10:04 -->
<meta http-equiv="Content-Type" content="text/html;charset=utf-8" />
<title>Designing Complementary filters for sensor fusion using $\mathcal{H}_\infty$ synthesis - Matlab Computation</title>
<meta name="author" content="Dehaeze Thomas" />
<meta name="generator" content="Org Mode" />
<link rel="stylesheet" type="text/css" href="https://research.tdehaeze.xyz/css/style.css"/>
<script type="text/javascript" src="https://research.tdehaeze.xyz/js/script.js"></script>
<script>
MathJax = {
svg: {
scale: 1,
fontCache: "global"
},
tex: {
tags: "ams",
multlineWidth: "%MULTLINEWIDTH",
tagSide: "right",
macros: {bm: ["\\boldsymbol{#1}",1],},
tagIndent: ".8em"
}
};
</script>
<script id="MathJax-script" async
src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-svg.js"></script>
</head>
<body>
<div id="org-div-home-and-up">
<a accesskey="h" href="../index.html"> UP </a>
|
<a accesskey="H" href="../index.html"> HOME </a>
</div><div id="content" class="content">
<h1 class="title">Designing Complementary filters for sensor fusion using \(\mathcal{H}_\infty\) synthesis - Matlab Computation</h1>
<div id="table-of-contents" role="doc-toc">
<h2>Table of Contents</h2>
<div id="text-table-of-contents" role="doc-toc">
<ul>
<li><a href="#sec:h_inf_synthesis_complementary_filters">1. H-Infinity synthesis of complementary filters</a>
<ul>
<li><a href="#orgc4b4c6d">1.1. Synthesis Architecture</a></li>
<li><a href="#org99141ab">1.2. Design of Weighting Function - Proposed formula</a></li>
<li><a href="#orge755bd5">1.3. Weighting functions for the design of two complementary filters</a></li>
<li><a href="#orgbd5024b">1.4. Synthesis of the complementary filters</a></li>
<li><a href="#org8eadcab">1.5. Obtained Complementary Filters</a></li>
</ul>
</li>
<li><a href="#sec:comp_filters_ligo">2. Design of complementary filters used in the Active Vibration Isolation System at the LIGO</a>
<ul>
<li><a href="#org775cee5">2.1. Specifications</a></li>
<li><a href="#org6402809">2.2. FIR Filter</a></li>
<li><a href="#orge47e4d1">2.3. Weighting function design</a></li>
<li><a href="#org5ef288a">2.4. Synthesis of the complementary filters</a></li>
<li><a href="#org71076fb">2.5. Comparison of the FIR filters and synthesized filters</a></li>
</ul>
</li>
<li><a href="#sec:closed_loop_complementary_filters">3. “Closed-Loop” complementary filters</a>
<ul>
<li><a href="#orgfa47886">3.1. Weighting Function design</a></li>
<li><a href="#org43ccb7c">3.2. Generalized plant</a></li>
<li><a href="#orgbf556a9">3.3. Synthesis of the closed-loop complementary filters</a></li>
<li><a href="#org426fd90">3.4. Synthesized filters</a></li>
</ul>
</li>
<li><a href="#sec:three_comp_filters">4. Synthesis of three complementary filters</a>
<ul>
<li><a href="#org23dc1a0">4.1. Synthesis Architecture</a></li>
<li><a href="#orgf36e7cb">4.2. Weights</a></li>
<li><a href="#org8bb1bfb">4.3. H-Infinity Synthesis</a></li>
</ul>
</li>
<li><a href="#sec:matlab_scripts">5. Matlab Scripts</a>
<ul>
<li><a href="#sec:1_synthesis_complementary_filters">5.1. <code>1_synthesis_complementary_filters.m</code></a></li>
<li><a href="#sec:2_ligo_complementary_filters">5.2. <code>2_ligo_complementary_filters.m</code></a></li>
<li><a href="#sec:3_closed_loop_complementary_filters">5.3. <code>3_closed_loop_complementary_filters.m</code></a></li>
<li><a href="#sec:4_three_complementary_filters">5.4. <code>4_three_complementary_filters.m</code></a></li>
<li><a href="#sec:generateWF">5.5. <code>generateWF</code>: Generate Weighting Functions</a></li>
<li><a href="#sec:generateCF">5.6. <code>generateCF</code>: Generate Complementary Filters</a></li>
</ul>
</li>
</ul>
</div>
</div>
<hr>
<p>This report is also available as a <a href="./dehaeze21_desig_compl_filte_matlab.pdf">pdf</a>.</p>
<hr>
<p>
The present document is a companion file for the journal paper (<a href="#citeproc_bib_item_1">Dehaeze, Vermat, and Collette 2021</a>).
All the Matlab (<a href="#citeproc_bib_item_5">MATLAB 2020</a>) scripts used in the paper are here shared and explained.
</p>
<p>
This document is divided into the following sections also corresponding to the paper sections:
</p>
<ul class="org-ul">
<li>Section <a href="#sec:h_inf_synthesis_complementary_filters">1</a>: the shaping of complementary filters is written as an \(\mathcal{H}_\infty\) optimization problem using weighting functions. The weighting function design is discussed and the method is applied for the design of a set of simple complementary filters.</li>
<li>Section <a href="#sec:comp_filters_ligo">2</a>: the effectiveness of the proposed complementary filter synthesis strategy is demonstrated by designing complex complementary filters used in the first isolation stage at the LIGO</li>
<li>Section <a href="#sec:closed_loop_complementary_filters">3</a>: complementary filters are designed using the classical feedback loop</li>
<li>Section <a href="#sec:three_comp_filters">4</a>: the proposed design method is generalized for the design of a set of three complementary filters</li>
<li>Section <a href="#sec:matlab_scripts">5</a>: complete Matlab scripts and functions developed are listed</li>
</ul>
<div id="outline-container-sec:h_inf_synthesis_complementary_filters" class="outline-2">
<h2 id="sec:h_inf_synthesis_complementary_filters"><span class="section-number-2">1.</span> H-Infinity synthesis of complementary filters</h2>
<div class="outline-text-2" id="text-sec:h_inf_synthesis_complementary_filters">
</div>
<div id="outline-container-orgc4b4c6d" class="outline-3">
<h3 id="orgc4b4c6d"><span class="section-number-3">1.1.</span> Synthesis Architecture</h3>
<div class="outline-text-3" id="text-1-1">
<p>
In order to generate two complementary filters with a wanted shape, the generalized plant of Figure <a href="#org938abd0">1</a> can be used.
The included weights \(W_1(s)\) and \(W_2(s)\) are used to specify the upper bounds of the complementary filters being generated.
</p>
<div id="org938abd0" class="figure">
<p><img src="figs-journal/h_infinity_robust_fusion_plant.png" alt="h_infinity_robust_fusion_plant.png" />
</p>
<p><span class="figure-number">Figure 1: </span>Generalized plant used for the \(\mathcal{H}_\infty\) synthesis of a set of two complementary fiters</p>
</div>
<p>
Applied the standard \(\mathcal{H}_\infty\) synthesis on this generalized plant will give a transfer function \(H_2(s)\) (see Figure <a href="#org133e437">2</a>) such that the \(\mathcal{H}_\infty\) norm of the transfer function from \(w\) to \([z_1,\ z_2]\) is less than one \eqref{eq:h_inf_objective}.
</p>
<div id="org133e437" class="figure">
<p><img src="figs-journal/h_infinity_robust_fusion_fb.png" alt="h_infinity_robust_fusion_fb.png" />
</p>
<p><span class="figure-number">Figure 2: </span>Generalized plant with the synthesized filter obtained after the \(\mathcal{H}_\infty\) synthesis</p>
</div>
\begin{equation}
\left\| \begin{array}{c} (1 - H_2(s)) W_1(s) \\ H_2(s) W_2(s) \end{array} \right\|_\infty < 1 \label{eq:h_inf_objective}
\end{equation}
<p>
Thus, if the synthesis is successful and the above condition is verified, we can define \(H_1(s)\) to be the complementary of \(H_2(s)\) \eqref{eq:H1_complementary_of_H2} and we have condition \eqref{eq:shaping_comp_filters} verified.
</p>
\begin{equation}
H_1(s) = 1 - H_2(s) \label{eq:H1_complementary_of_H2}
\end{equation}
\begin{equation}
\left\| \begin{array}{c} H_1(s) W_1(s) \\ H_2(s) W_2(s) \end{array} \right\|_\infty < 1
\quad \Longrightarrow \quad
\left\{
\begin{array}{c}
|H_1(j\omega)| < \frac{1}{|W_1(j\omega)|}, \quad \forall \omega \\
|H_2(j\omega)| < \frac{1}{|W_2(j\omega)|}, \quad \forall \omega
\end{array}
\right. \label{eq:shaping_comp_filters}
\end{equation}
<p>
We then see that \(W_1(s)\) and \(W_2(s)\) can be used to set the wanted upper bounds of the magnitudes of both \(H_1(s)\) and \(H_2(s)\).
</p>
<p>
The presented synthesis method therefore allows to shape two filters \(H_1(s)\) and \(H_2(s)\) \eqref{eq:shaping_comp_filters} while ensuring their complementary property \eqref{eq:H1_complementary_of_H2}.
</p>
<p>
The complete Matlab script for this part is given in Section <a href="#sec:1_synthesis_complementary_filters">5.1</a>.
</p>
</div>
</div>
<div id="outline-container-org99141ab" class="outline-3">
<h3 id="org99141ab"><span class="section-number-3">1.2.</span> Design of Weighting Function - Proposed formula</h3>
<div class="outline-text-3" id="text-1-2">
<p>
A formula is proposed to help the design of the weighting functions:
</p>
\begin{equation}
W(s) = \left( \frac{
\frac{1}{\omega_0} \sqrt{\frac{1 - \left(\frac{G_0}{G_c}\right)^{\frac{2}{n}}}{1 - \left(\frac{G_c}{G_\infty}\right)^{\frac{2}{n}}}} s + \left(\frac{G_0}{G_c}\right)^{\frac{1}{n}}
}{
\left(\frac{1}{G_\infty}\right)^{\frac{1}{n}} \frac{1}{\omega_0} \sqrt{\frac{1 - \left(\frac{G_0}{G_c}\right)^{\frac{2}{n}}}{1 - \left(\frac{G_c}{G_\infty}\right)^{\frac{2}{n}}}} s + \left(\frac{1}{G_c}\right)^{\frac{1}{n}}
}\right)^n \label{eq:weighting_function_formula}
\end{equation}
<p>
The parameters permits to specify:
</p>
<ul class="org-ul">
<li>the low frequency gain: \(G_0 = lim_{\omega \to 0} |W(j\omega)|\)</li>
<li>the high frequency gain: \(G_\infty = lim_{\omega \to \infty} |W(j\omega)|\)</li>
<li>the absolute gain at \(\omega_0\): \(G_c = |W(j\omega_0)|\)</li>
<li>the absolute slope between high and low frequency: \(n\)</li>
</ul>
<p>
The general shape of a weighting function generated using the formula is shown in figure <a href="#org652005a">3</a>.
</p>
<div id="org652005a" class="figure">
<p><img src="figs/weight_formula.png" alt="weight_formula.png" />
</p>
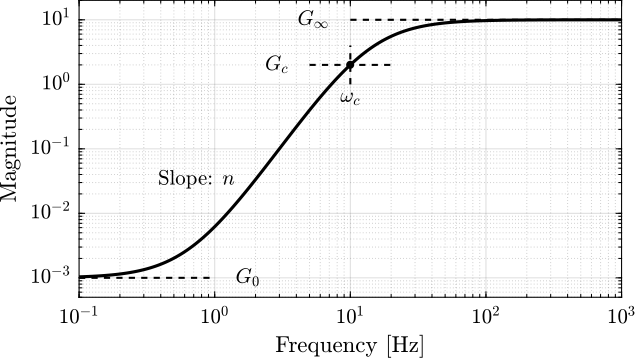
<p><span class="figure-number">Figure 3: </span>Magnitude of the weighting function generated using formula \eqref{eq:weighting_function_formula}</p>
</div>
</div>
</div>
<div id="outline-container-orge755bd5" class="outline-3">
<h3 id="orge755bd5"><span class="section-number-3">1.3.</span> Weighting functions for the design of two complementary filters</h3>
<div class="outline-text-3" id="text-1-3">
<p>
<a id="orgbf8ba5a"></a>
</p>
<p>
The weighting function formula \eqref{eq:weighting_function_formula} is used to generate the upper bounds of two complementary filters that we wish to design.
</p>
<p>
The matlab function <code>generateWF</code> is described in Section <a href="#sec:generateWF">5.5</a>.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Design of the Weighting Functions</span>
W1 = generateWF(<span class="org-string">'n'</span>, 3, <span class="org-string">'w0'</span>, 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>10, <span class="org-string">'G0'</span>, 1000, <span class="org-string">'Ginf'</span>, 1<span class="org-builtin">/</span>10, <span class="org-string">'Gc'</span>, 0.45);
W2 = generateWF(<span class="org-string">'n'</span>, 2, <span class="org-string">'w0'</span>, 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>10, <span class="org-string">'G0'</span>, 1<span class="org-builtin">/</span>10, <span class="org-string">'Ginf'</span>, 1000, <span class="org-string">'Gc'</span>, 0.45);
</pre>
</div>
<p>
The inverse magnitude of these two weighting functions are shown in Figure <a href="#org9dd5099">4</a>.
</p>
<div id="org9dd5099" class="figure">
<p><img src="figs/weights_W1_W2.png" alt="weights_W1_W2.png" />
</p>
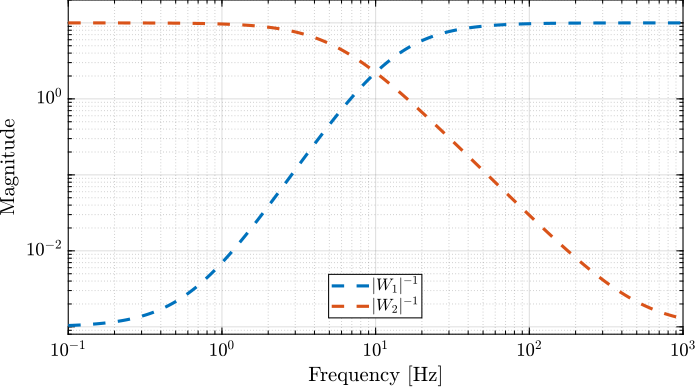
<p><span class="figure-number">Figure 4: </span>Inverse magnitude of the design weighting functions</p>
</div>
</div>
</div>
<div id="outline-container-orgbd5024b" class="outline-3">
<h3 id="orgbd5024b"><span class="section-number-3">1.4.</span> Synthesis of the complementary filters</h3>
<div class="outline-text-3" id="text-1-4">
<p>
The generalized plant of Figure <a href="#org938abd0">1</a> is defined as follows:
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Generalized Plant</span>
P = [W1 <span class="org-builtin">-</span>W1;
0 W2;
1 0];
</pre>
</div>
<p>
And the \(\mathcal{H}_\infty\) synthesis is performed using the <code>hinfsyn</code> command.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% H-Infinity Synthesis</span>
[H2, <span class="org-builtin">~</span>, gamma, <span class="org-builtin">~</span>] = hinfsyn(P, 1, 1,<span class="org-string">'TOLGAM'</span>, 0.001, <span class="org-string">'METHOD'</span>, <span class="org-string">'ric'</span>, <span class="org-string">'DISPLAY'</span>, <span class="org-string">'on'</span>);
</pre>
</div>
<pre class="example" id="orge151ac9">
[H2, ~, gamma, ~] = hinfsyn(P, 1, 1,'TOLGAM', 0.001, 'METHOD', 'ric', 'DISPLAY', 'on');
Test bounds: 0.3223 <= gamma <= 1000
gamma X>=0 Y>=0 rho(XY)<1 p/f
1.795e+01 1.4e-07 0.0e+00 1.481e-16 p
2.406e+00 1.4e-07 0.0e+00 3.604e-15 p
8.806e-01 -3.1e+02 # -1.4e-16 7.370e-19 f
1.456e+00 1.4e-07 0.0e+00 1.499e-18 p
1.132e+00 1.4e-07 0.0e+00 8.587e-15 p
9.985e-01 1.4e-07 0.0e+00 2.331e-13 p
9.377e-01 -7.7e+02 # -6.6e-17 3.744e-14 f
9.676e-01 -2.0e+03 # -5.7e-17 1.046e-13 f
9.829e-01 -6.6e+03 # -1.1e-16 2.949e-13 f
9.907e-01 1.4e-07 0.0e+00 2.374e-19 p
9.868e-01 -1.6e+04 # -6.4e-17 5.331e-14 f
9.887e-01 -5.1e+04 # -1.5e-17 2.703e-19 f
9.897e-01 1.4e-07 0.0e+00 1.583e-11 p
Limiting gains...
9.897e-01 1.5e-07 0.0e+00 1.183e-12 p
9.897e-01 6.9e-07 0.0e+00 1.365e-12 p
Best performance (actual): 0.9897
</pre>
<p>
As shown above, the obtained \(\mathcal{H}_\infty\) norm of the transfer function from \(w\) to \([z_1,\ z_2]\) is found to be less than one meaning the synthesis is successful.
</p>
<p>
We then define the filter \(H_1(s)\) to be the complementary of \(H_2(s)\) \eqref{eq:H1_complementary_of_H2}.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Define H1 to be the complementary of H2</span>
H1 = 1 <span class="org-builtin">-</span> H2;
</pre>
</div>
<p>
The function <code>generateCF</code> can also be used to synthesize the complementary filters.
This function is described in Section <a href="#sec:generateCF">5.6</a>.
</p>
<div class="org-src-container">
<pre class="src src-matlab">[H1, H2] = generateCF(W1, W2);
</pre>
</div>
</div>
</div>
<div id="outline-container-org8eadcab" class="outline-3">
<h3 id="org8eadcab"><span class="section-number-3">1.5.</span> Obtained Complementary Filters</h3>
<div class="outline-text-3" id="text-1-5">
<p>
The obtained complementary filters are shown below and are found to be of order 5.
Their bode plots are shown in figure <a href="#org2c627be">5</a> and compare with the defined upper bounds.
</p>
<pre class="example" id="orgfedb8df">
zpk(H1)
ans =
(s+1.289e05) (s+153.6) (s+3.842)^3
-------------------------------------------------------
(s+1.29e05) (s^2 + 102.1s + 2733) (s^2 + 69.45s + 3272)
zpk(H2)
ans =
125.61 (s+3358)^2 (s^2 + 46.61s + 813.8)
-------------------------------------------------------
(s+1.29e05) (s^2 + 102.1s + 2733) (s^2 + 69.45s + 3272)
</pre>
<div id="org2c627be" class="figure">
<p><img src="figs/hinf_filters_results.png" alt="hinf_filters_results.png" />
</p>
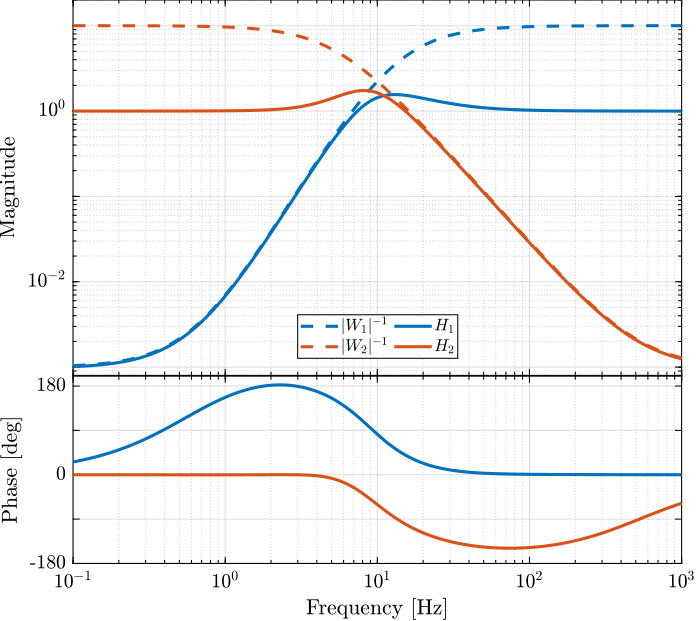
<p><span class="figure-number">Figure 5: </span>Obtained complementary filters using \(\mathcal{H}_\infty\) synthesis</p>
</div>
</div>
</div>
</div>
<div id="outline-container-sec:comp_filters_ligo" class="outline-2">
<h2 id="sec:comp_filters_ligo"><span class="section-number-2">2.</span> Design of complementary filters used in the Active Vibration Isolation System at the LIGO</h2>
<div class="outline-text-2" id="text-sec:comp_filters_ligo">
<p>
In this section, the proposed method for the design of complementary filters is validated for the design of a set of two complex complementary filters used for the first isolation stage at the LIGO (<a href="#citeproc_bib_item_3">Hua, Adhikari, et al. 2004</a>).
</p>
<p>
The complete Matlab script for this part is given in Section <a href="#sec:2_ligo_complementary_filters">5.2</a>.
</p>
</div>
<div id="outline-container-org775cee5" class="outline-3">
<h3 id="org775cee5"><span class="section-number-3">2.1.</span> Specifications</h3>
<div class="outline-text-3" id="text-2-1">
<p>
The specifications for the set of complementary filters (\(L_1,H_1\)) used at the LIGO are summarized below (for further details, refer to (<a href="#citeproc_bib_item_4">Hua, Debra, et al. 2004</a>)):
</p>
<ul class="org-ul">
<li>From 0 to 0.008 Hz, the magnitude \(|L_1(j\omega)|\) should be less or equal to \(8 \times 10^{-4}\)</li>
<li>Between 0.008 Hz to 0.04 Hz, the filter \(L_1(s)\) should attenuate the input signal proportional to frequency cubed</li>
<li>Between 0.04 Hz to 0.1 Hz, the magnitude \(|L_1(j\omega)|\) should be less than \(3\)</li>
<li>Above 0.1 Hz, the magnitude \(|H_1(j\omega)|\) should be less than \(0.045\)</li>
</ul>
<p>
The specifications are translated into upper bounds of the complementary filters and are shown in Figure <a href="#org03607c6">6</a>.
</p>
<div id="org03607c6" class="figure">
<p><img src="figs/ligo_specifications.png" alt="ligo_specifications.png" />
</p>
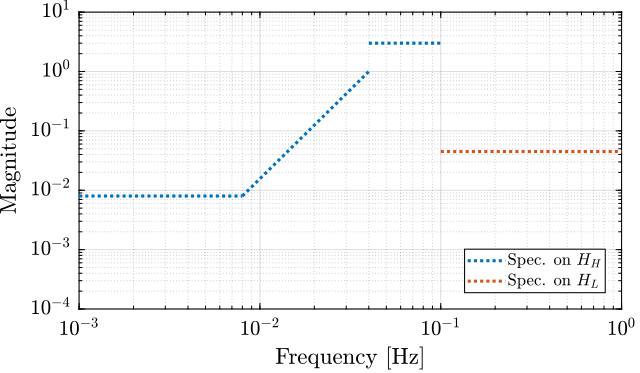
<p><span class="figure-number">Figure 6: </span>Specification for the LIGO complementary filters</p>
</div>
</div>
</div>
<div id="outline-container-org6402809" class="outline-3">
<h3 id="org6402809"><span class="section-number-3">2.2.</span> FIR Filter</h3>
<div class="outline-text-3" id="text-2-2">
<p>
To replicated the complementary filters developed in (<a href="#citeproc_bib_item_3">Hua, Adhikari, et al. 2004</a>), the CVX Matlab toolbox (<a href="#citeproc_bib_item_2">Grant and Boyd 2014</a>) is used.
</p>
<p>
The CVX toolbox is initialized and the <code>SeDuMi</code> solver (<a href="#citeproc_bib_item_6">Sturm 1999</a>) is used.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Initialized CVX</span>
cvx_startup;
cvx_solver sedumi;
</pre>
</div>
<p>
We define the frequency vectors on which we will constrain the norm of the FIR filter.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Frequency vectors</span>
w1 = 0<span class="org-builtin">:</span>4.06e<span class="org-builtin">-</span>4<span class="org-builtin">:</span>0.008;
w2 = 0.008<span class="org-builtin">:</span>4.06e<span class="org-builtin">-</span>4<span class="org-builtin">:</span>0.04;
w3 = 0.04<span class="org-builtin">:</span>8.12e<span class="org-builtin">-</span>4<span class="org-builtin">:</span>0.1;
w4 = 0.1<span class="org-builtin">:</span>8.12e<span class="org-builtin">-</span>4<span class="org-builtin">:</span>0.83;
</pre>
</div>
<p>
The order \(n\) of the FIR filter is defined.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Filter order</span>
n = 512;
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Initialization of filter responses</span>
A1 = [ones(length(w1),1), cos(kron(w1<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
A2 = [ones(length(w2),1), cos(kron(w2<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
A3 = [ones(length(w3),1), cos(kron(w3<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
A4 = [ones(length(w4),1), cos(kron(w4<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
B1 = [zeros(length(w1),1), sin(kron(w1<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
B2 = [zeros(length(w2),1), sin(kron(w2<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
B3 = [zeros(length(w3),1), sin(kron(w3<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
B4 = [zeros(length(w4),1), sin(kron(w4<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
</pre>
</div>
<p>
And the convex optimization is run.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Convex optimization</span>
cvx_begin
variable y(n<span class="org-builtin">+</span>1,1)
<span class="org-comment-delimiter">% </span><span class="org-comment">t</span>
maximize(<span class="org-builtin">-</span>y(1))
<span class="org-keyword">for</span> <span class="org-variable-name"><span class="org-matlab-math">i</span></span> = <span class="org-constant">1:length(w1)</span>
norm([0 A1(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>); 0 B1(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>)]<span class="org-builtin">*</span>y) <span class="org-builtin"><=</span> 8e<span class="org-builtin">-</span>3;
<span class="org-keyword">end</span>
<span class="org-keyword">for</span> <span class="org-variable-name"><span class="org-matlab-math">i</span></span> = <span class="org-constant">1:length(w2)</span>
norm([0 A2(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>); 0 B2(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>)]<span class="org-builtin">*</span>y) <span class="org-builtin"><=</span> 8e<span class="org-builtin">-</span>3<span class="org-builtin">*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>w2(<span class="org-matlab-math">i</span>)<span class="org-builtin">/</span>(0.008<span class="org-builtin">*</span>2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>))<span class="org-builtin">^</span>3;
<span class="org-keyword">end</span>
<span class="org-keyword">for</span> <span class="org-variable-name"><span class="org-matlab-math">i</span></span> = <span class="org-constant">1:length(w3)</span>
norm([0 A3(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>); 0 B3(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>)]<span class="org-builtin">*</span>y) <span class="org-builtin"><=</span> 3;
<span class="org-keyword">end</span>
<span class="org-keyword">for</span> <span class="org-variable-name"><span class="org-matlab-math">i</span></span> = <span class="org-constant">1:length(w4)</span>
norm([[1 0]<span class="org-builtin">'-</span> [0 A4(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>); 0 B4(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>)]<span class="org-builtin">*</span>y]) <span class="org-builtin"><=</span> y(1);
<span class="org-keyword">end</span>
cvx_end
h = y(2<span class="org-builtin">:</span>end);
</pre>
</div>
<pre class="example" id="orge5b954e">
cvx_begin
variable y(n+1,1)
% t
maximize(-y(1))
for i = 1:length(w1)
norm([0 A1(i,:); 0 B1(i,:)]*y) <= 8e-3;
end
for i = 1:length(w2)
norm([0 A2(i,:); 0 B2(i,:)]*y) <= 8e-3*(2*pi*w2(i)/(0.008*2*pi))^3;
end
for i = 1:length(w3)
norm([0 A3(i,:); 0 B3(i,:)]*y) <= 3;
end
for i = 1:length(w4)
norm([[1 0]'- [0 A4(i,:); 0 B4(i,:)]*y]) <= y(1);
end
cvx_end
Calling SeDuMi 1.34: 4291 variables, 1586 equality constraints
For improved efficiency, SeDuMi is solving the dual problem.
------------------------------------------------------------
SeDuMi 1.34 (beta) by AdvOL, 2005-2008 and Jos F. Sturm, 1998-2003.
Alg = 2: xz-corrector, Adaptive Step-Differentiation, theta = 0.250, beta = 0.500
eqs m = 1586, order n = 3220, dim = 4292, blocks = 1073
nnz(A) = 1100727 + 0, nnz(ADA) = 1364794, nnz(L) = 683190
it : b*y gap delta rate t/tP* t/tD* feas cg cg prec
0 : 4.11E+02 0.000
1 : -2.58E+00 1.25E+02 0.000 0.3049 0.9000 0.9000 4.87 1 1 3.0E+02
2 : -2.36E+00 3.90E+01 0.000 0.3118 0.9000 0.9000 1.83 1 1 6.6E+01
3 : -1.69E+00 1.31E+01 0.000 0.3354 0.9000 0.9000 1.76 1 1 1.5E+01
4 : -8.60E-01 7.10E+00 0.000 0.5424 0.9000 0.9000 2.48 1 1 4.8E+00
5 : -4.91E-01 5.44E+00 0.000 0.7661 0.9000 0.9000 3.12 1 1 2.5E+00
6 : -2.96E-01 3.88E+00 0.000 0.7140 0.9000 0.9000 2.62 1 1 1.4E+00
7 : -1.98E-01 2.82E+00 0.000 0.7271 0.9000 0.9000 2.14 1 1 8.5E-01
8 : -1.39E-01 2.00E+00 0.000 0.7092 0.9000 0.9000 1.78 1 1 5.4E-01
9 : -9.99E-02 1.30E+00 0.000 0.6494 0.9000 0.9000 1.51 1 1 3.3E-01
10 : -7.57E-02 8.03E-01 0.000 0.6175 0.9000 0.9000 1.31 1 1 2.0E-01
11 : -5.99E-02 4.22E-01 0.000 0.5257 0.9000 0.9000 1.17 1 1 1.0E-01
12 : -5.28E-02 2.45E-01 0.000 0.5808 0.9000 0.9000 1.08 1 1 5.9E-02
13 : -4.82E-02 1.28E-01 0.000 0.5218 0.9000 0.9000 1.05 1 1 3.1E-02
14 : -4.56E-02 5.65E-02 0.000 0.4417 0.9045 0.9000 1.02 1 1 1.4E-02
15 : -4.43E-02 2.41E-02 0.000 0.4265 0.9004 0.9000 1.01 1 1 6.0E-03
16 : -4.37E-02 8.90E-03 0.000 0.3690 0.9070 0.9000 1.00 1 1 2.3E-03
17 : -4.35E-02 3.24E-03 0.000 0.3641 0.9164 0.9000 1.00 1 1 9.5E-04
18 : -4.34E-02 1.55E-03 0.000 0.4788 0.9086 0.9000 1.00 1 1 4.7E-04
19 : -4.34E-02 8.77E-04 0.000 0.5653 0.9169 0.9000 1.00 1 1 2.8E-04
20 : -4.34E-02 5.05E-04 0.000 0.5754 0.9034 0.9000 1.00 1 1 1.6E-04
21 : -4.34E-02 2.94E-04 0.000 0.5829 0.9136 0.9000 1.00 1 1 9.9E-05
22 : -4.34E-02 1.63E-04 0.015 0.5548 0.9000 0.0000 1.00 1 1 6.6E-05
23 : -4.33E-02 9.42E-05 0.000 0.5774 0.9053 0.9000 1.00 1 1 3.9E-05
24 : -4.33E-02 6.27E-05 0.000 0.6658 0.9148 0.9000 1.00 1 1 2.6E-05
25 : -4.33E-02 3.75E-05 0.000 0.5972 0.9187 0.9000 1.00 1 1 1.6E-05
26 : -4.33E-02 1.89E-05 0.000 0.5041 0.9117 0.9000 1.00 1 1 8.6E-06
27 : -4.33E-02 9.72E-06 0.000 0.5149 0.9050 0.9000 1.00 1 1 4.5E-06
28 : -4.33E-02 2.94E-06 0.000 0.3021 0.9194 0.9000 1.00 1 1 1.5E-06
29 : -4.33E-02 9.73E-07 0.000 0.3312 0.9189 0.9000 1.00 2 2 5.3E-07
30 : -4.33E-02 2.82E-07 0.000 0.2895 0.9063 0.9000 1.00 2 2 1.6E-07
31 : -4.33E-02 8.05E-08 0.000 0.2859 0.9049 0.9000 1.00 2 2 4.7E-08
32 : -4.33E-02 1.43E-08 0.000 0.1772 0.9059 0.9000 1.00 2 2 8.8E-09
iter seconds digits c*x b*y
32 49.4 6.8 -4.3334083581e-02 -4.3334090214e-02
|Ax-b| = 3.7e-09, [Ay-c]_+ = 1.1E-10, |x|= 1.0e+00, |y|= 2.6e+00
Detailed timing (sec)
Pre IPM Post
3.902E+00 4.576E+01 1.035E-02
Max-norms: ||b||=1, ||c|| = 3,
Cholesky |add|=0, |skip| = 0, ||L.L|| = 4.26267.
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): -0.0433341
h = y(2:end);
</pre>
<p>
Finally, the filter response is computed over the frequency vector defined and the result is shown on figure <a href="#orgf5ce15e">7</a> which is very close to the filters obtain in (<a href="#citeproc_bib_item_3">Hua, Adhikari, et al. 2004</a>).
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Combine the frequency vectors to form the obtained filter</span>
w = [w1 w2 w3 w4];
H = [exp(<span class="org-builtin">-</span><span class="org-matlab-math">j</span><span class="org-builtin">*</span>kron(w<span class="org-builtin">'.*</span>2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>,[0<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))]<span class="org-builtin">*</span>h;
</pre>
</div>
<div id="orgf5ce15e" class="figure">
<p><img src="figs/fir_filter_ligo.png" alt="fir_filter_ligo.png" />
</p>
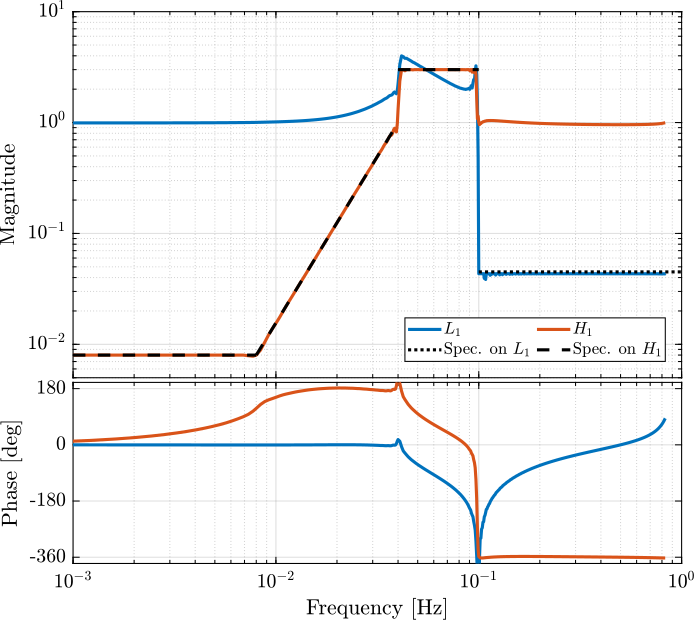
<p><span class="figure-number">Figure 7: </span>FIR Complementary filters obtain after convex optimization</p>
</div>
</div>
</div>
<div id="outline-container-orge47e4d1" class="outline-3">
<h3 id="orge47e4d1"><span class="section-number-3">2.3.</span> Weighting function design</h3>
<div class="outline-text-3" id="text-2-3">
<p>
The weightings function that will be used for the \(\mathcal{H}_\infty\) synthesis of the complementary filters are now designed.
</p>
<p>
These weights will determine the order of the obtained filters.
</p>
<p>
Here are the requirements on the filters:
</p>
<ul class="org-ul">
<li>reasonable order</li>
<li>to be as close as possible to the specified upper bounds</li>
<li>stable and minimum phase</li>
</ul>
<p>
The weighting function for the High Pass filter is defined as follows:
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Design of the weight for the high pass filter</span>
w1 = 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>0.008; x1 = 0.35;
w2 = 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>0.04; x2 = 0.5;
w3 = 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>0.05; x3 = 0.5;
<span class="org-comment-delimiter">% </span><span class="org-comment">Slope of +3 from w1</span>
wH = 0.008<span class="org-builtin">*</span>(s<span class="org-builtin">^</span>2<span class="org-builtin">/</span>w1<span class="org-builtin">^</span>2 <span class="org-builtin">+</span> 2<span class="org-builtin">*</span>x1<span class="org-builtin">/</span>w1<span class="org-builtin">*</span>s <span class="org-builtin">+</span> 1)<span class="org-builtin">*</span>(s<span class="org-builtin">/</span>w1 <span class="org-builtin">+</span> 1);
<span class="org-comment-delimiter">% </span><span class="org-comment">Little bump from w2 to w3</span>
wH = wH<span class="org-builtin">*</span>(s<span class="org-builtin">^</span>2<span class="org-builtin">/</span>w2<span class="org-builtin">^</span>2 <span class="org-builtin">+</span> 2<span class="org-builtin">*</span>x2<span class="org-builtin">/</span>w2<span class="org-builtin">*</span>s <span class="org-builtin">+</span> 1)<span class="org-builtin">/</span>(s<span class="org-builtin">^</span>2<span class="org-builtin">/</span>w3<span class="org-builtin">^</span>2 <span class="org-builtin">+</span> 2<span class="org-builtin">*</span>x3<span class="org-builtin">/</span>w3<span class="org-builtin">*</span>s <span class="org-builtin">+</span> 1);
<span class="org-comment-delimiter">% </span><span class="org-comment">No Slope at high frequencies</span>
wH = wH<span class="org-builtin">/</span>(s<span class="org-builtin">^</span>2<span class="org-builtin">/</span>w3<span class="org-builtin">^</span>2 <span class="org-builtin">+</span> 2<span class="org-builtin">*</span>x3<span class="org-builtin">/</span>w3<span class="org-builtin">*</span>s <span class="org-builtin">+</span> 1)<span class="org-builtin">/</span>(s<span class="org-builtin">/</span>w3 <span class="org-builtin">+</span> 1);
<span class="org-comment-delimiter">% </span><span class="org-comment">Little bump between w2 and w3</span>
w0 = 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>0.045; xi = 0.1; A = 2; n = 1;
wH = wH<span class="org-builtin">*</span>((s<span class="org-builtin">^</span>2 <span class="org-builtin">+</span> 2<span class="org-builtin">*</span>w0<span class="org-builtin">*</span>xi<span class="org-builtin">*</span>A<span class="org-builtin">^</span>(1<span class="org-builtin">/</span>n)<span class="org-builtin">*</span>s <span class="org-builtin">+</span> w0<span class="org-builtin">^</span>2)<span class="org-builtin">/</span>(s<span class="org-builtin">^</span>2 <span class="org-builtin">+</span> 2<span class="org-builtin">*</span>w0<span class="org-builtin">*</span>xi<span class="org-builtin">*</span>s <span class="org-builtin">+</span> w0<span class="org-builtin">^</span>2))<span class="org-builtin">^</span>n;
wH = 1<span class="org-builtin">/</span>wH;
wH = minreal(ss(wH));
</pre>
</div>
<p>
And the weighting function for the Low pass filter is taken as a Chebyshev Type I filter.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Design of the weight for the low pass filter</span>
n = 20; <span class="org-comment-delimiter">% </span><span class="org-comment">Filter order</span>
Rp = 1; <span class="org-comment-delimiter">% </span><span class="org-comment">Peak to peak passband ripple</span>
Wp = 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>0.102; <span class="org-comment-delimiter">% </span><span class="org-comment">Edge frequency</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">Chebyshev Type I filter design</span>
[b,a] = cheby1(n, Rp, Wp, <span class="org-string">'high'</span>, <span class="org-string">'s'</span>);
wL = 0.04<span class="org-builtin">*</span>tf(a, b);
wL = 1<span class="org-builtin">/</span>wL;
wL = minreal(ss(wL));
</pre>
</div>
<p>
The inverse magnitude of the weighting functions are shown in Figure <a href="#org588a935">8</a>.
</p>
<div id="org588a935" class="figure">
<p><img src="figs/ligo_weights.png" alt="ligo_weights.png" />
</p>
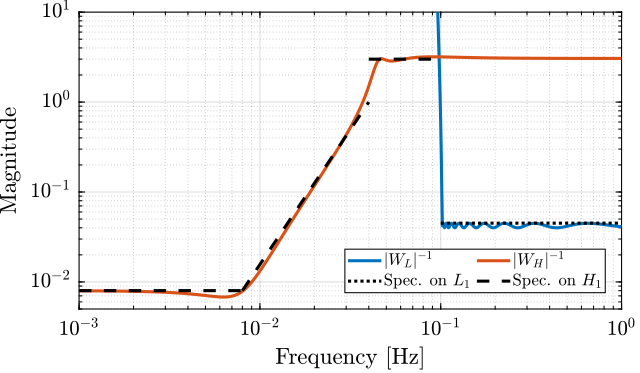
<p><span class="figure-number">Figure 8: </span>Weights for the \(\mathcal{H}_\infty\) synthesis</p>
</div>
</div>
</div>
<div id="outline-container-org5ef288a" class="outline-3">
<h3 id="org5ef288a"><span class="section-number-3">2.4.</span> Synthesis of the complementary filters</h3>
<div class="outline-text-3" id="text-2-4">
<p>
The generalized plant of figure <a href="#org938abd0">1</a> is defined.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Generalized plant for the H-infinity Synthesis</span>
P = [0 wL;
wH <span class="org-builtin">-</span>wH;
1 0];
</pre>
</div>
<p>
And the standard \(\mathcal{H}_\infty\) synthesis using the <code>hinfsyn</code> command is performed.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Standard H-Infinity synthesis</span>
[Hl, <span class="org-builtin">~</span>, gamma, <span class="org-builtin">~</span>] = hinfsyn(P, 1, 1,<span class="org-string">'TOLGAM'</span>, 0.001, <span class="org-string">'METHOD'</span>, <span class="org-string">'ric'</span>, <span class="org-string">'DISPLAY'</span>, <span class="org-string">'on'</span>);
</pre>
</div>
<pre class="example" id="org12089e0">
[Hl, ~, gamma, ~] = hinfsyn(P, 1, 1,'TOLGAM', 0.001, 'METHOD', 'ric', 'DISPLAY', 'on');
Resetting value of Gamma min based on D_11, D_12, D_21 terms
Test bounds: 0.3276 < gamma <= 1.8063
gamma hamx_eig xinf_eig hamy_eig yinf_eig nrho_xy p/f
1.806 1.4e-02 -1.7e-16 3.6e-03 -4.8e-12 0.0000 p
1.067 1.3e-02 -4.2e-14 3.6e-03 -1.9e-12 0.0000 p
0.697 1.3e-02 -3.0e-01# 3.6e-03 -3.5e-11 0.0000 f
0.882 1.3e-02 -9.5e-01# 3.6e-03 -1.2e-34 0.0000 f
0.975 1.3e-02 -2.7e+00# 3.6e-03 -1.6e-12 0.0000 f
1.021 1.3e-02 -8.7e+00# 3.6e-03 -4.5e-16 0.0000 f
1.044 1.3e-02 -6.5e-14 3.6e-03 -3.0e-15 0.0000 p
1.032 1.3e-02 -1.8e+01# 3.6e-03 0.0e+00 0.0000 f
1.038 1.3e-02 -3.8e+01# 3.6e-03 0.0e+00 0.0000 f
1.041 1.3e-02 -8.3e+01# 3.6e-03 -2.9e-33 0.0000 f
1.042 1.3e-02 -1.9e+02# 3.6e-03 -3.4e-11 0.0000 f
1.043 1.3e-02 -5.3e+02# 3.6e-03 -7.5e-13 0.0000 f
Gamma value achieved: 1.0439
</pre>
<p>
The obtained \(\mathcal{H}_\infty\) norm is found to be close than one meaning the synthesis is successful.
</p>
<p>
The high pass filter \(H_H(s)\) is defined to be the complementary of the synthesized low pass filter \(H_L(s)\):
</p>
\begin{equation}
H_H(s) = 1 - H_L(s)
\end{equation}
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% High pass filter as the complementary of the low pass filter</span>
Hh = 1 <span class="org-builtin">-</span> Hl;
</pre>
</div>
<p>
The size of the filters is shown to be equal to the sum of the weighting functions orders.
</p>
<pre class="example" id="org7e59413">
size(Hh), size(Hl)
State-space model with 1 outputs, 1 inputs, and 27 states.
State-space model with 1 outputs, 1 inputs, and 27 states.
</pre>
<p>
The magnitude of the obtained filters as well as the requirements are shown in Figure <a href="#orgb9b3d25">9</a>.
</p>
<div id="orgb9b3d25" class="figure">
<p><img src="figs/hinf_synthesis_ligo_results.png" alt="hinf_synthesis_ligo_results.png" />
</p>
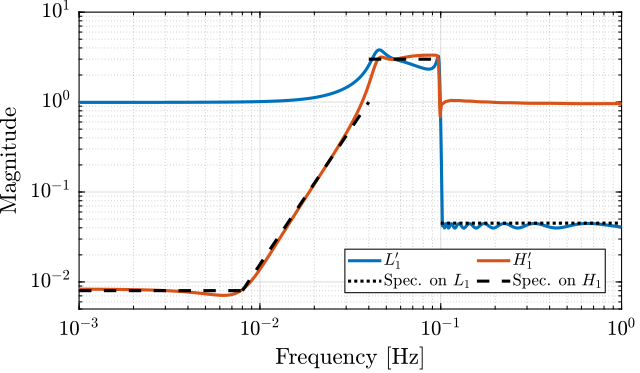
<p><span class="figure-number">Figure 9: </span>Obtained complementary filters using the \(\mathcal{H}_\infty\) synthesis</p>
</div>
</div>
</div>
<div id="outline-container-org71076fb" class="outline-3">
<h3 id="org71076fb"><span class="section-number-3">2.5.</span> Comparison of the FIR filters and synthesized filters</h3>
<div class="outline-text-3" id="text-2-5">
<p>
Let’s now compare the FIR filters designed in (<a href="#citeproc_bib_item_3">Hua, Adhikari, et al. 2004</a>) with the with complementary filters obtained with the \(\mathcal{H}_\infty\) synthesis.
</p>
<p>
This is done in Figure <a href="#org7eeadda">10</a>, and both set of filters are found to be very close to each other.
</p>
<div id="org7eeadda" class="figure">
<p><img src="figs/comp_fir_ligo_hinf.png" alt="comp_fir_ligo_hinf.png" />
</p>
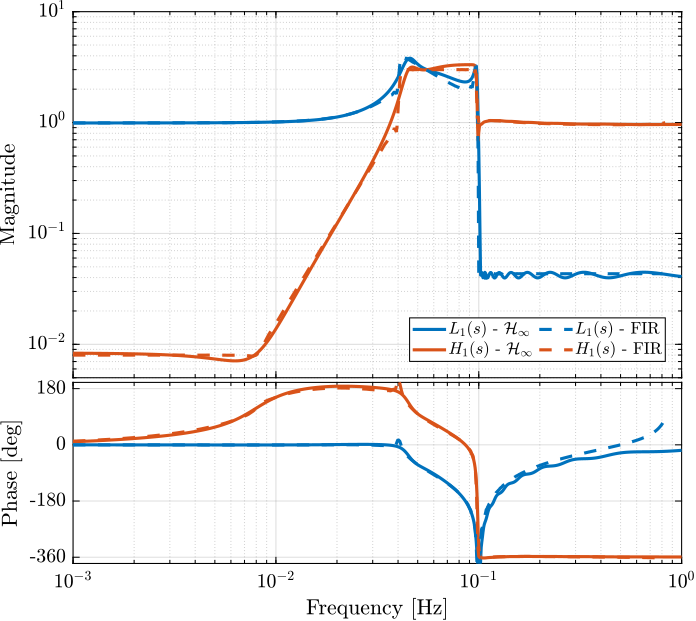
<p><span class="figure-number">Figure 10: </span>Comparison between the FIR filters developped for LIGO and the \(\mathcal{H}_\infty\) complementary filters</p>
</div>
</div>
</div>
</div>
<div id="outline-container-sec:closed_loop_complementary_filters" class="outline-2">
<h2 id="sec:closed_loop_complementary_filters"><span class="section-number-2">3.</span> “Closed-Loop” complementary filters</h2>
<div class="outline-text-2" id="text-sec:closed_loop_complementary_filters">
<p>
In this section, the classical feedback architecture shown in Figure <a href="#org91711eb">11</a> is used for the design of complementary filters.
</p>
<div id="org91711eb" class="figure">
<p><img src="figs-journal/feedback_sensor_fusion.png" alt="feedback_sensor_fusion.png" />
</p>
<p><span class="figure-number">Figure 11: </span>“Closed-Loop” complementary filters</p>
</div>
<p>
The complete Matlab script for this part is given in Section <a href="#sec:3_closed_loop_complementary_filters">5.3</a>.
</p>
</div>
<div id="outline-container-orgfa47886" class="outline-3">
<h3 id="orgfa47886"><span class="section-number-3">3.1.</span> Weighting Function design</h3>
<div class="outline-text-3" id="text-3-1">
<p>
Weighting functions using the <code>generateWF</code> Matlab function are designed to specify the upper bounds of the complementary filters to be designed.
These weighting functions are the same as the ones used in Section <a href="#orgbf8ba5a">1.3</a>.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Design of the Weighting Functions</span>
W1 = generateWF(<span class="org-string">'n'</span>, 3, <span class="org-string">'w0'</span>, 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>10, <span class="org-string">'G0'</span>, 1000, <span class="org-string">'Ginf'</span>, 1<span class="org-builtin">/</span>10, <span class="org-string">'Gc'</span>, 0.45);
W2 = generateWF(<span class="org-string">'n'</span>, 2, <span class="org-string">'w0'</span>, 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>10, <span class="org-string">'G0'</span>, 1<span class="org-builtin">/</span>10, <span class="org-string">'Ginf'</span>, 1000, <span class="org-string">'Gc'</span>, 0.45);
</pre>
</div>
</div>
</div>
<div id="outline-container-org43ccb7c" class="outline-3">
<h3 id="org43ccb7c"><span class="section-number-3">3.2.</span> Generalized plant</h3>
<div class="outline-text-3" id="text-3-2">
<p>
The generalized plant of Figure <a href="#org3a36382">12</a> is defined below:
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Generalized plant for "closed-loop" complementary filter synthesis</span>
P = [ W1 0 1;
<span class="org-builtin">-</span>W1 W2 <span class="org-builtin">-</span>1];
</pre>
</div>
<div id="org3a36382" class="figure">
<p><img src="figs-journal/feedback_synthesis_architecture_generalized_plant.png" alt="feedback_synthesis_architecture_generalized_plant.png" />
</p>
<p><span class="figure-number">Figure 12: </span>Generalized plant used for the \(\mathcal{H}_\infty\) synthesis of “closed-loop” complementary filters</p>
</div>
</div>
</div>
<div id="outline-container-orgbf556a9" class="outline-3">
<h3 id="orgbf556a9"><span class="section-number-3">3.3.</span> Synthesis of the closed-loop complementary filters</h3>
<div class="outline-text-3" id="text-3-3">
<p>
And the standard \(\mathcal{H}_\infty\) synthesis is performed.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Standard H-Infinity Synthesis</span>
[L, <span class="org-builtin">~</span>, gamma, <span class="org-builtin">~</span>] = hinfsyn(P, 1, 1,<span class="org-string">'TOLGAM'</span>, 0.001, <span class="org-string">'METHOD'</span>, <span class="org-string">'ric'</span>, <span class="org-string">'DISPLAY'</span>, <span class="org-string">'on'</span>);
</pre>
</div>
<pre class="example" id="org1af6c18">
Test bounds: 0.3191 <= gamma <= 1.669
gamma X>=0 Y>=0 rho(XY)<1 p/f
7.299e-01 -1.5e-19 -2.4e+01 # 1.555e-18 f
1.104e+00 0.0e+00 1.6e-07 2.037e-19 p
8.976e-01 -3.2e-16 -1.4e+02 # 5.561e-16 f
9.954e-01 0.0e+00 1.6e-07 1.041e-15 p
9.452e-01 -1.1e-15 -3.8e+02 # 4.267e-15 f
9.700e-01 -6.5e-16 -1.6e+03 # 9.876e-15 f
9.826e-01 0.0e+00 1.6e-07 8.775e-39 p
9.763e-01 -5.0e-16 -6.2e+03 # 3.519e-14 f
9.795e-01 0.0e+00 1.6e-07 6.971e-20 p
9.779e-01 -1.9e-31 -2.2e+04 # 5.600e-18 f
9.787e-01 0.0e+00 1.6e-07 5.546e-19 p
Limiting gains...
9.789e-01 0.0e+00 1.6e-07 1.084e-13 p
9.789e-01 0.0e+00 9.7e-07 1.137e-13 p
Best performance (actual): 0.9789
</pre>
</div>
</div>
<div id="outline-container-org426fd90" class="outline-3">
<h3 id="org426fd90"><span class="section-number-3">3.4.</span> Synthesized filters</h3>
<div class="outline-text-3" id="text-3-4">
<p>
The obtained filter \(L(s)\) can then be included in the feedback architecture shown in Figure <a href="#org9d40494">13</a>.
</p>
<p>
The closed-loop transfer functions from \(\hat{x}_1\) to \(\hat{x}\) and from \(\hat{x}_2\) to \(\hat{x}\) corresponding respectively to the sensitivity and complementary sensitivity transfer functions are defined below:
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Complementary filters</span>
H1 = inv(1 <span class="org-builtin">+</span> L);
H2 = 1 <span class="org-builtin">-</span> H1;
</pre>
</div>
<pre class="example" id="org8cae256">
zpk(H1) =
(s+3.842)^3 (s+153.6) (s+1.289e05)
-------------------------------------------------------
(s+1.29e05) (s^2 + 102.1s + 2733) (s^2 + 69.45s + 3272)
zpk(H2) =
125.61 (s+3358)^2 (s^2 + 46.61s + 813.8)
-------------------------------------------------------
(s+1.29e05) (s^2 + 102.1s + 2733) (s^2 + 69.45s + 3272)
</pre>
<p>
The bode plots of the synthesized complementary filters are compared with the upper bounds in Figure <a href="#org9d40494">13</a>.
</p>
<div id="org9d40494" class="figure">
<p><img src="figs/hinf_filters_results_mixed_sensitivity.png" alt="hinf_filters_results_mixed_sensitivity.png" />
</p>
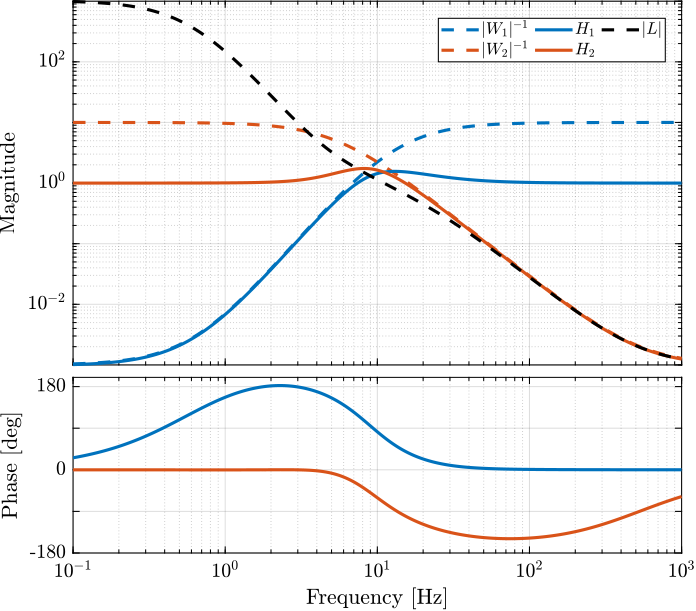
<p><span class="figure-number">Figure 13: </span>Bode plot of the obtained complementary filters</p>
</div>
</div>
</div>
</div>
<div id="outline-container-sec:three_comp_filters" class="outline-2">
<h2 id="sec:three_comp_filters"><span class="section-number-2">4.</span> Synthesis of three complementary filters</h2>
<div class="outline-text-2" id="text-sec:three_comp_filters">
<p>
In this section, the proposed synthesis method of complementary filters is generalized for the synthesis of a set of three complementary filters.
</p>
<p>
The complete Matlab script for this part is given in Section <a href="#sec:4_three_complementary_filters">5.4</a>.
</p>
</div>
<div id="outline-container-org23dc1a0" class="outline-3">
<h3 id="org23dc1a0"><span class="section-number-3">4.1.</span> Synthesis Architecture</h3>
<div class="outline-text-3" id="text-4-1">
<p>
The synthesis objective is to shape three filters that are complementary.
This corresponds to the conditions \eqref{eq:obj_three_cf} where \(W_1(s)\), \(W_2(s)\) and \(W_3(s)\) are weighting functions used to specify the maximum wanted magnitude of the three complementary filters.
</p>
\begin{equation}
\begin{aligned}
& |H_1(j\omega)| < \frac{1}{|W_1(j\omega)|}, \quad \forall\omega \\
& |H_2(j\omega)| < \frac{1}{|W_2(j\omega)|}, \quad \forall\omega \\
& |H_3(j\omega)| < \frac{1}{|W_3(j\omega)|}, \quad \forall\omega \\
& H_1(s) + H_2(s) + H_3(s) = 1
\end{aligned} \label{eq:obj_three_cf}
\end{equation}
<p>
This synthesis can be done by performing the standard \(\mathcal{H}_\infty\) synthesis with on the generalized plant in Figure <a href="#orge2e8c55">14</a>.
</p>
<div id="orge2e8c55" class="figure">
<p><img src="figs-journal/comp_filter_three_hinf_fb.png" alt="comp_filter_three_hinf_fb.png" />
</p>
<p><span class="figure-number">Figure 14: </span>Generalized architecture for generating 3 complementary filters</p>
</div>
<p>
After synthesis, filter \(H_2(s)\) and \(H_3(s)\) are obtained as shown in Figure <a href="#orge2e8c55">14</a>.
The last filter \(H_1(s)\) is defined as the complementary of the two others as in \eqref{eq:H1_complementary_of_H2_H3}.
</p>
\begin{equation}
H_1(s) = 1 - H_2(s) - H_3(s) \label{eq:H1_complementary_of_H2_H3}
\end{equation}
</div>
</div>
<div id="outline-container-orgf36e7cb" class="outline-3">
<h3 id="orgf36e7cb"><span class="section-number-3">4.2.</span> Weights</h3>
<div class="outline-text-3" id="text-4-2">
<p>
The three weighting functions are defined as shown below.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Design of the Weighting Functions</span>
W1 = generateWF(<span class="org-string">'n'</span>, 2, <span class="org-string">'w0'</span>, 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>1, <span class="org-string">'G0'</span>, 1<span class="org-builtin">/</span>10, <span class="org-string">'Ginf'</span>, 1000, <span class="org-string">'Gc'</span>, 0.5);
W2 = 0.22<span class="org-builtin">*</span>(1 <span class="org-builtin">+</span> s<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">/</span>1)<span class="org-builtin">^</span>2<span class="org-builtin">/</span>(sqrt(1e<span class="org-builtin">-</span>4) <span class="org-builtin">+</span> s<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">/</span>1)<span class="org-builtin">^</span>2<span class="org-builtin">*</span>(1 <span class="org-builtin">+</span> s<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">/</span>10)<span class="org-builtin">^</span>2<span class="org-builtin">/</span>(1 <span class="org-builtin">+</span> s<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">/</span>1000)<span class="org-builtin">^</span>2;
W3 = generateWF(<span class="org-string">'n'</span>, 3, <span class="org-string">'w0'</span>, 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>10, <span class="org-string">'G0'</span>, 1000, <span class="org-string">'Ginf'</span>, 1<span class="org-builtin">/</span>10, <span class="org-string">'Gc'</span>, 0.5);
</pre>
</div>
<p>
Their inverse magnitudes are displayed in Figure <a href="#orga89c5b8">15</a>.
</p>
<div id="orga89c5b8" class="figure">
<p><img src="figs/three_weighting_functions.png" alt="three_weighting_functions.png" />
</p>
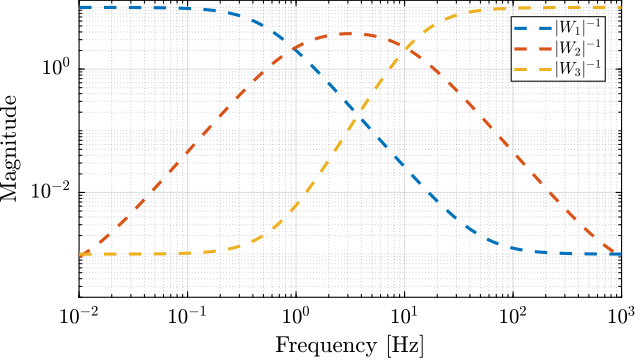
<p><span class="figure-number">Figure 15: </span>Three weighting functions used for the \(\mathcal{H}_\infty\) synthesis of the complementary filters</p>
</div>
</div>
</div>
<div id="outline-container-org8bb1bfb" class="outline-3">
<h3 id="org8bb1bfb"><span class="section-number-3">4.3.</span> H-Infinity Synthesis</h3>
<div class="outline-text-3" id="text-4-3">
<p>
The generalized plant in Figure <a href="#orge2e8c55">14</a> containing the weighting functions is defined below.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Generalized plant for the synthesis of 3 complementary filters</span>
P = [W1 <span class="org-builtin">-</span>W1 <span class="org-builtin">-</span>W1;
0 W2 0 ;
0 0 W3;
1 0 0];
</pre>
</div>
<p>
And the standard \(\mathcal{H}_\infty\) synthesis using the <code>hinfsyn</code> command is performed.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% Standard H-Infinity Synthesis</span>
[H, <span class="org-builtin">~</span>, gamma, <span class="org-builtin">~</span>] = hinfsyn(P, 1, 2,<span class="org-string">'TOLGAM'</span>, 0.001, <span class="org-string">'METHOD'</span>, <span class="org-string">'ric'</span>, <span class="org-string">'DISPLAY'</span>, <span class="org-string">'on'</span>);
</pre>
</div>
<pre class="example" id="orgbeefca4">
Resetting value of Gamma min based on D_11, D_12, D_21 terms
Test bounds: 0.1000 < gamma <= 1050.0000
gamma hamx_eig xinf_eig hamy_eig yinf_eig nrho_xy p/f
1.050e+03 3.2e+00 4.5e-13 6.3e-02 -1.2e-11 0.0000 p
525.050 3.2e+00 1.3e-13 6.3e-02 0.0e+00 0.0000 p
262.575 3.2e+00 2.1e-12 6.3e-02 -1.5e-13 0.0000 p
131.337 3.2e+00 1.1e-12 6.3e-02 -7.2e-29 0.0000 p
65.719 3.2e+00 2.0e-12 6.3e-02 0.0e+00 0.0000 p
32.909 3.2e+00 7.4e-13 6.3e-02 -5.9e-13 0.0000 p
16.505 3.2e+00 1.4e-12 6.3e-02 0.0e+00 0.0000 p
8.302 3.2e+00 1.6e-12 6.3e-02 0.0e+00 0.0000 p
4.201 3.2e+00 1.6e-12 6.3e-02 0.0e+00 0.0000 p
2.151 3.2e+00 1.6e-12 6.3e-02 0.0e+00 0.0000 p
1.125 3.2e+00 2.8e-12 6.3e-02 0.0e+00 0.0000 p
0.613 3.0e+00 -2.5e+03# 6.3e-02 0.0e+00 0.0000 f
0.869 3.1e+00 -2.9e+01# 6.3e-02 0.0e+00 0.0000 f
0.997 3.2e+00 1.9e-12 6.3e-02 0.0e+00 0.0000 p
0.933 3.1e+00 -6.9e+02# 6.3e-02 0.0e+00 0.0000 f
0.965 3.1e+00 -3.0e+03# 6.3e-02 0.0e+00 0.0000 f
0.981 3.1e+00 -8.6e+03# 6.3e-02 0.0e+00 0.0000 f
0.989 3.2e+00 -2.7e+04# 6.3e-02 0.0e+00 0.0000 f
0.993 3.2e+00 -5.7e+05# 6.3e-02 0.0e+00 0.0000 f
0.995 3.2e+00 2.2e-12 6.3e-02 0.0e+00 0.0000 p
0.994 3.2e+00 1.6e-12 6.3e-02 0.0e+00 0.0000 p
0.994 3.2e+00 1.0e-12 6.3e-02 0.0e+00 0.0000 p
Gamma value achieved: 0.9936
</pre>
<p>
The two synthesized filters \(H_2(s)\) and \(H_3(s)\) are defined below:
And the third filter \(H_1(s)\) is defined using \eqref{eq:H1_complementary_of_H2_H3}.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak">%% H1 is defined as the complementary filter of H2 and H3</span>
H1 = 1 <span class="org-builtin">-</span> H2 <span class="org-builtin">-</span> H3;
</pre>
</div>
<p>
The bode plots of the three obtained complementary filters are shown in Figure <a href="#orgd7996d8">16</a>.
</p>
<div id="orgd7996d8" class="figure">
<p><img src="figs/three_complementary_filters_results.png" alt="three_complementary_filters_results.png" />
</p>
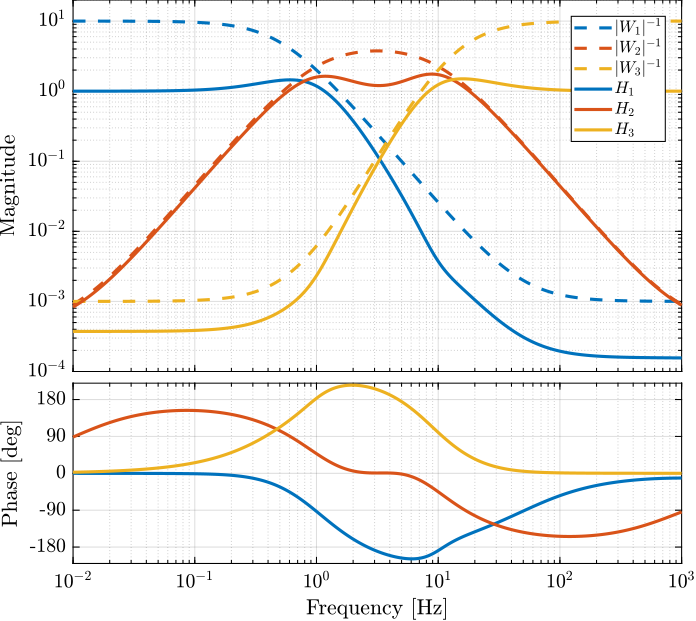
<p><span class="figure-number">Figure 16: </span>The three complementary filters obtained after \(\mathcal{H}_\infty\) synthesis</p>
</div>
</div>
</div>
</div>
<div id="outline-container-sec:matlab_scripts" class="outline-2">
<h2 id="sec:matlab_scripts"><span class="section-number-2">5.</span> Matlab Scripts</h2>
<div class="outline-text-2" id="text-sec:matlab_scripts">
</div>
<div id="outline-container-sec:1_synthesis_complementary_filters" class="outline-3">
<h3 id="sec:1_synthesis_complementary_filters"><span class="section-number-3">5.1.</span> <code>1_synthesis_complementary_filters.m</code></h3>
<div class="outline-text-3" id="text-sec:1_synthesis_complementary_filters">
<p>
This scripts corresponds to section 3 of (<a href="#citeproc_bib_item_1">Dehaeze, Vermat, and Collette 2021</a>).
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="linenr"> 1: </span><span class="org-matlab-cellbreak">%% Clear Workspace and Close figures</span>
<span class="linenr"> 2: </span>clear; close <span class="org-builtin">all</span>; clc;
<span class="linenr"> 3: </span>
<span class="linenr"> 4: </span><span class="org-matlab-cellbreak">%% Intialize Laplace variable</span>
<span class="linenr"> 5: </span>s = zpk(<span class="org-string">'s'</span>);
<span class="linenr"> 6: </span>
<span class="linenr"> 7: </span><span class="org-matlab-cellbreak">%% Initialize Frequency Vector</span>
<span class="linenr"> 8: </span>freqs = logspace(<span class="org-builtin">-</span>1, 3, 1000);
<span class="linenr"> 9: </span>
<span class="linenr"> 10: </span><span class="org-matlab-cellbreak">%% Weighting Function Design</span>
<span class="linenr"> 11: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Parameters</span>
<span class="linenr"> 12: </span>n = 3; w0 = 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>10; G0 = 1e<span class="org-builtin">-</span>3; G1 = 1e1; Gc = 2;
<span class="linenr"> 13: </span>
<span class="linenr"> 14: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Formulas</span>
<span class="linenr"> 15: </span>W = (((1<span class="org-builtin">/</span>w0)<span class="org-builtin">*</span>sqrt((1<span class="org-builtin">-</span>(G0<span class="org-builtin">/</span>Gc)<span class="org-builtin">^</span>(2<span class="org-builtin">/</span>n))<span class="org-builtin">/</span>(1<span class="org-builtin">-</span>(Gc<span class="org-builtin">/</span>G1)<span class="org-builtin">^</span>(2<span class="org-builtin">/</span>n)))<span class="org-builtin">*</span>s <span class="org-builtin">+</span> (G0<span class="org-builtin">/</span>Gc)<span class="org-builtin">^</span>(1<span class="org-builtin">/</span>n))<span class="org-builtin">/</span>((1<span class="org-builtin">/</span>G1)<span class="org-builtin">^</span>(1<span class="org-builtin">/</span>n)<span class="org-builtin">*</span>(1<span class="org-builtin">/</span>w0)<span class="org-builtin">*</span>sqrt((1<span class="org-builtin">-</span>(G0<span class="org-builtin">/</span>Gc)<span class="org-builtin">^</span>(2<span class="org-builtin">/</span>n))<span class="org-builtin">/</span>(1<span class="org-builtin">-</span>(Gc<span class="org-builtin">/</span>G1)<span class="org-builtin">^</span>(2<span class="org-builtin">/</span>n)))<span class="org-builtin">*</span>s <span class="org-builtin">+</span> (1<span class="org-builtin">/</span>Gc)<span class="org-builtin">^</span>(1<span class="org-builtin">/</span>n)))<span class="org-builtin">^</span>n;
<span class="linenr"> 16: </span>
<span class="linenr"> 17: </span><span class="org-matlab-cellbreak">%% Magnitude of the weighting function with parameters</span>
<span class="linenr"> 18: </span><span class="org-builtin">figure</span>;
<span class="linenr"> 19: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr"> 20: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(W, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'k-'</span>);
<span class="linenr"> 21: </span>
<span class="linenr"> 22: </span><span class="org-builtin">plot</span>([1e<span class="org-builtin">-</span>3 1e0], [G0 G0], <span class="org-string">'k--'</span>, <span class="org-string">'LineWidth'</span>, 1)
<span class="linenr"> 23: </span><span class="org-builtin">text</span>(1e0, G0, <span class="org-string">'$\quad G_0$'</span>)
<span class="linenr"> 24: </span>
<span class="linenr"> 25: </span><span class="org-builtin">plot</span>([1e1 1e3], [G1 G1], <span class="org-string">'k--'</span>, <span class="org-string">'LineWidth'</span>, 1)
<span class="linenr"> 26: </span><span class="org-builtin">text</span>(1e1,G1,<span class="org-string">'$G_{\infty}\quad$'</span>,<span class="org-string">'HorizontalAlignment'</span>, <span class="org-string">'right'</span>)
<span class="linenr"> 27: </span>
<span class="linenr"> 28: </span><span class="org-builtin">plot</span>([w0<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span> w0<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span>], [1 2<span class="org-builtin">*</span>Gc], <span class="org-string">'k--'</span>, <span class="org-string">'LineWidth'</span>, 1)
<span class="linenr"> 29: </span><span class="org-builtin">text</span>(w0<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span>,1,<span class="org-string">'$\omega_c$'</span>,<span class="org-string">'VerticalAlignment'</span>, <span class="org-string">'top'</span>, <span class="org-string">'HorizontalAlignment'</span>, <span class="org-string">'center'</span>)
<span class="linenr"> 30: </span>
<span class="linenr"> 31: </span><span class="org-builtin">plot</span>([w0<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">/</span>2 2<span class="org-builtin">*</span>w0<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span>], [Gc Gc], <span class="org-string">'k--'</span>, <span class="org-string">'LineWidth'</span>, 1)
<span class="linenr"> 32: </span><span class="org-builtin">text</span>(w0<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">/</span>2, Gc, <span class="org-string">'$G_c \quad$'</span>,<span class="org-string">'HorizontalAlignment'</span>, <span class="org-string">'right'</span>)
<span class="linenr"> 33: </span>
<span class="linenr"> 34: </span><span class="org-builtin">text</span>(w0<span class="org-builtin">/</span>5<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">/</span>2, abs(evalfr(W, <span class="org-matlab-math">j</span><span class="org-builtin">*</span>w0<span class="org-builtin">/</span>5)), <span class="org-string">'Slope: $n \quad$'</span>, <span class="org-string">'HorizontalAlignment'</span>, <span class="org-string">'right'</span>)
<span class="linenr"> 35: </span>
<span class="linenr"> 36: </span><span class="org-builtin">text</span>(w0<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span>, abs(evalfr(W, <span class="org-matlab-math">j</span><span class="org-builtin">*</span>w0)), <span class="org-string">'$\bullet$'</span>, <span class="org-string">'HorizontalAlignment'</span>, <span class="org-string">'center'</span>)
<span class="linenr"> 37: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>); <span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'YScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr"> 38: </span><span class="org-builtin">xlabel</span>(<span class="org-string">'Frequency [Hz]'</span>); <span class="org-builtin">ylabel</span>(<span class="org-string">'Magnitude'</span>);
<span class="linenr"> 39: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr"> 40: </span><span class="org-builtin">xlim</span>([freqs(1), freqs(end)]);
<span class="linenr"> 41: </span><span class="org-builtin">ylim</span>([5e<span class="org-builtin">-</span>4, 20]);
<span class="linenr"> 42: </span>yticks([1e<span class="org-builtin">-</span>4, 1e<span class="org-builtin">-</span>3, 1e<span class="org-builtin">-</span>2, 1e<span class="org-builtin">-</span>1, 1, 1e1]);
<span class="linenr"> 43: </span>
<span class="linenr"> 44: </span><span class="org-matlab-cellbreak">%% Design of the Weighting Functions</span>
<span class="linenr"> 45: </span>W1 = generateWF(<span class="org-string">'n'</span>, 3, <span class="org-string">'w0'</span>, 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>10, <span class="org-string">'G0'</span>, 1000, <span class="org-string">'Ginf'</span>, 1<span class="org-builtin">/</span>10, <span class="org-string">'Gc'</span>, 0.45);
<span class="linenr"> 46: </span>W2 = generateWF(<span class="org-string">'n'</span>, 2, <span class="org-string">'w0'</span>, 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>10, <span class="org-string">'G0'</span>, 1<span class="org-builtin">/</span>10, <span class="org-string">'Ginf'</span>, 1000, <span class="org-string">'Gc'</span>, 0.45);
<span class="linenr"> 47: </span>
<span class="linenr"> 48: </span><span class="org-matlab-cellbreak">%% Plot of the Weighting function magnitude</span>
<span class="linenr"> 49: </span><span class="org-builtin">figure</span>;
<span class="linenr"> 50: </span><span class="org-builtin">tiledlayout</span>(1, 1, <span class="org-string">'TileSpacing'</span>, <span class="org-string">'None'</span>, <span class="org-string">'Padding'</span>, <span class="org-string">'None'</span>);
<span class="linenr"> 51: </span>ax1 = <span class="org-builtin">nexttile</span>();
<span class="linenr"> 52: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr"> 53: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr"> 54: </span><span class="org-builtin">plot</span>(freqs, 1<span class="org-builtin">./</span>abs(squeeze(freqresp(W1, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_1|^{-1}$'</span>);
<span class="linenr"> 55: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr"> 56: </span><span class="org-builtin">plot</span>(freqs, 1<span class="org-builtin">./</span>abs(squeeze(freqresp(W2, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_2|^{-1}$'</span>);
<span class="linenr"> 57: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>); <span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'YScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr"> 58: </span><span class="org-builtin">xlabel</span>(<span class="org-string">'Frequency [Hz]'</span>, <span class="org-string">'FontSize'</span>, 10); <span class="org-builtin">ylabel</span>(<span class="org-string">'Magnitude'</span>, <span class="org-string">'FontSize'</span>, 10);
<span class="linenr"> 59: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr"> 60: </span><span class="org-builtin">xlim</span>([freqs(1), freqs(end)]);
<span class="linenr"> 61: </span>xticks([0.1, 1, 10, 100, 1000]);
<span class="linenr"> 62: </span><span class="org-builtin">ylim</span>([8e<span class="org-builtin">-</span>4, 20]);
<span class="linenr"> 63: </span>yticks([1e<span class="org-builtin">-</span>3, 1e<span class="org-builtin">-</span>2, 1e<span class="org-builtin">-</span>1, 1, 1e1]);
<span class="linenr"> 64: </span>yticklabels({<span class="org-string">''</span>, <span class="org-string">'$10^{-2}$'</span>, <span class="org-string">''</span>, <span class="org-string">'$10^0$'</span>, <span class="org-string">''</span>});
<span class="linenr"> 65: </span>ax1.FontSize = 9;
<span class="linenr"> 66: </span>leg = <span class="org-builtin">legend</span>(<span class="org-string">'location'</span>, <span class="org-string">'south'</span>, <span class="org-string">'FontSize'</span>, 8);
<span class="linenr"> 67: </span>leg.ItemTokenSize(1) = 18;
<span class="linenr"> 68: </span>
<span class="linenr"> 69: </span><span class="org-matlab-cellbreak">%% Generalized Plant</span>
<span class="linenr"> 70: </span>P = [W1 <span class="org-builtin">-</span>W1;
<span class="linenr"> 71: </span> 0 W2;
<span class="linenr"> 72: </span> 1 0];
<span class="linenr"> 73: </span>
<span class="linenr"> 74: </span><span class="org-matlab-cellbreak">%% H-Infinity Synthesis</span>
<span class="linenr"> 75: </span>[H2, <span class="org-builtin">~</span>, gamma, <span class="org-builtin">~</span>] = hinfsyn(P, 1, 1,<span class="org-string">'TOLGAM'</span>, 0.001, <span class="org-string">'METHOD'</span>, <span class="org-string">'ric'</span>, <span class="org-string">'DISPLAY'</span>, <span class="org-string">'on'</span>);
<span class="linenr"> 76: </span>
<span class="linenr"> 77: </span><span class="org-matlab-cellbreak">%% Define H1 to be the complementary of H2</span>
<span class="linenr"> 78: </span>H1 = 1 <span class="org-builtin">-</span> H2;
<span class="linenr"> 79: </span>
<span class="linenr"> 80: </span><span class="org-matlab-cellbreak">%% Bode plot of the complementary filters</span>
<span class="linenr"> 81: </span><span class="org-builtin">figure</span>;
<span class="linenr"> 82: </span><span class="org-builtin">tiledlayout</span>(3, 1, <span class="org-string">'TileSpacing'</span>, <span class="org-string">'None'</span>, <span class="org-string">'Padding'</span>, <span class="org-string">'None'</span>);
<span class="linenr"> 83: </span>
<span class="linenr"> 84: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Magnitude</span>
<span class="linenr"> 85: </span>ax1 = <span class="org-builtin">nexttile</span>([2, 1]);
<span class="linenr"> 86: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr"> 87: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr"> 88: </span><span class="org-builtin">plot</span>(freqs, 1<span class="org-builtin">./</span>abs(squeeze(freqresp(W1, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_1|^{-1}$'</span>);
<span class="linenr"> 89: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr"> 90: </span><span class="org-builtin">plot</span>(freqs, 1<span class="org-builtin">./</span>abs(squeeze(freqresp(W2, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_2|^{-1}$'</span>);
<span class="linenr"> 91: </span>
<span class="linenr"> 92: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr"> 93: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(H1, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$H_1$'</span>);
<span class="linenr"> 94: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr"> 95: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(H2, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$H_2$'</span>);
<span class="linenr"> 96: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr"> 97: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>); <span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'YScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr"> 98: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XTickLabel'</span>,[]); <span class="org-builtin">ylabel</span>(<span class="org-string">'Magnitude'</span>);
<span class="linenr"> 99: </span><span class="org-builtin">ylim</span>([8e<span class="org-builtin">-</span>4, 20]);
<span class="linenr">100: </span>yticks([1e<span class="org-builtin">-</span>3, 1e<span class="org-builtin">-</span>2, 1e<span class="org-builtin">-</span>1, 1, 1e1]);
<span class="linenr">101: </span>yticklabels({<span class="org-string">''</span>, <span class="org-string">'$10^{-2}$'</span>, <span class="org-string">''</span>, <span class="org-string">'$10^0$'</span>, <span class="org-string">''</span>})
<span class="linenr">102: </span>leg = <span class="org-builtin">legend</span>(<span class="org-string">'location'</span>, <span class="org-string">'south'</span>, <span class="org-string">'FontSize'</span>, 8, <span class="org-string">'NumColumns'</span>, 2);
<span class="linenr">103: </span>leg.ItemTokenSize(1) = 18;
<span class="linenr">104: </span>
<span class="linenr">105: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Phase</span>
<span class="linenr">106: </span>ax2 = <span class="org-builtin">nexttile</span>;
<span class="linenr">107: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr">108: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr">109: </span><span class="org-builtin">plot</span>(freqs, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>phase(squeeze(freqresp(H1, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>);
<span class="linenr">110: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr">111: </span><span class="org-builtin">plot</span>(freqs, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>phase(squeeze(freqresp(H2, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>);
<span class="linenr">112: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr">113: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">114: </span><span class="org-builtin">xlabel</span>(<span class="org-string">'Frequency [Hz]'</span>); <span class="org-builtin">ylabel</span>(<span class="org-string">'Phase [deg]'</span>);
<span class="linenr">115: </span>yticks([<span class="org-builtin">-</span>180<span class="org-builtin">:</span>90<span class="org-builtin">:</span>180]);
<span class="linenr">116: </span><span class="org-builtin">ylim</span>([<span class="org-builtin">-</span>180, 200])
<span class="linenr">117: </span>yticklabels({<span class="org-string">'-180'</span>, <span class="org-string">''</span>, <span class="org-string">'0'</span>, <span class="org-string">''</span>, <span class="org-string">'180'</span>})
<span class="linenr">118: </span>
<span class="linenr">119: </span>linkaxes([ax1,ax2],<span class="org-string">'x'</span>);
<span class="linenr">120: </span><span class="org-builtin">xlim</span>([freqs(1), freqs(end)]);
</pre>
</div>
</div>
</div>
<div id="outline-container-sec:2_ligo_complementary_filters" class="outline-3">
<h3 id="sec:2_ligo_complementary_filters"><span class="section-number-3">5.2.</span> <code>2_ligo_complementary_filters.m</code></h3>
<div class="outline-text-3" id="text-sec:2_ligo_complementary_filters">
<p>
This scripts corresponds to section 4 of (<a href="#citeproc_bib_item_1">Dehaeze, Vermat, and Collette 2021</a>).
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="linenr"> 1: </span><span class="org-matlab-cellbreak">%% Clear Workspace and Close figures</span>
<span class="linenr"> 2: </span>clear; close <span class="org-builtin">all</span>; clc;
<span class="linenr"> 3: </span>
<span class="linenr"> 4: </span><span class="org-matlab-cellbreak">%% Intialize Laplace variable</span>
<span class="linenr"> 5: </span>s = zpk(<span class="org-string">'s'</span>);
<span class="linenr"> 6: </span>
<span class="linenr"> 7: </span><span class="org-matlab-cellbreak">%% Initialize Frequency Vector</span>
<span class="linenr"> 8: </span>freqs = logspace(<span class="org-builtin">-</span>3, 0, 1000);
<span class="linenr"> 9: </span>
<span class="linenr"> 10: </span><span class="org-matlab-cellbreak">%% Upper bounds for the complementary filters</span>
<span class="linenr"> 11: </span><span class="org-builtin">figure</span>;
<span class="linenr"> 12: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr"> 13: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr"> 14: </span><span class="org-builtin">plot</span>([0.0001, 0.008], [8e<span class="org-builtin">-</span>3, 8e<span class="org-builtin">-</span>3], <span class="org-string">':'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'Spec. on $H_H$'</span>);
<span class="linenr"> 15: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr"> 16: </span><span class="org-builtin">plot</span>([0.008 0.04], [8e<span class="org-builtin">-</span>3, 1], <span class="org-string">':'</span>, <span class="org-string">'HandleVisibility'</span>, <span class="org-string">'off'</span>);
<span class="linenr"> 17: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr"> 18: </span><span class="org-builtin">plot</span>([0.04 0.1], [3, 3], <span class="org-string">':'</span>, <span class="org-string">'HandleVisibility'</span>, <span class="org-string">'off'</span>);
<span class="linenr"> 19: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr"> 20: </span><span class="org-builtin">plot</span>([0.1, 10], [0.045, 0.045], <span class="org-string">':'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'Spec. on $H_L$'</span>);
<span class="linenr"> 21: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>); <span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'YScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr"> 22: </span><span class="org-builtin">xlabel</span>(<span class="org-string">'Frequency [Hz]'</span>); <span class="org-builtin">ylabel</span>(<span class="org-string">'Magnitude'</span>);
<span class="linenr"> 23: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr"> 24: </span><span class="org-builtin">xlim</span>([freqs(1), freqs(end)]);
<span class="linenr"> 25: </span><span class="org-builtin">ylim</span>([1e<span class="org-builtin">-</span>4, 10]);
<span class="linenr"> 26: </span>leg = <span class="org-builtin">legend</span>(<span class="org-string">'location'</span>, <span class="org-string">'southeast'</span>, <span class="org-string">'FontSize'</span>, 8);
<span class="linenr"> 27: </span>leg.ItemTokenSize(1) = 18;
<span class="linenr"> 28: </span>
<span class="linenr"> 29: </span><span class="org-matlab-cellbreak">%% Initialized CVX</span>
<span class="linenr"> 30: </span>cvx_startup;
<span class="linenr"> 31: </span>cvx_solver sedumi;
<span class="linenr"> 32: </span>
<span class="linenr"> 33: </span><span class="org-matlab-cellbreak">%% Frequency vectors</span>
<span class="linenr"> 34: </span>w1 = 0<span class="org-builtin">:</span>4.06e<span class="org-builtin">-</span>4<span class="org-builtin">:</span>0.008;
<span class="linenr"> 35: </span>w2 = 0.008<span class="org-builtin">:</span>4.06e<span class="org-builtin">-</span>4<span class="org-builtin">:</span>0.04;
<span class="linenr"> 36: </span>w3 = 0.04<span class="org-builtin">:</span>8.12e<span class="org-builtin">-</span>4<span class="org-builtin">:</span>0.1;
<span class="linenr"> 37: </span>w4 = 0.1<span class="org-builtin">:</span>8.12e<span class="org-builtin">-</span>4<span class="org-builtin">:</span>0.83;
<span class="linenr"> 38: </span>
<span class="linenr"> 39: </span><span class="org-matlab-cellbreak">%% Filter order</span>
<span class="linenr"> 40: </span>n = 512;
<span class="linenr"> 41: </span>
<span class="linenr"> 42: </span><span class="org-matlab-cellbreak">%% Initialization of filter responses</span>
<span class="linenr"> 43: </span>A1 = [ones(length(w1),1), cos(kron(w1<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
<span class="linenr"> 44: </span>A2 = [ones(length(w2),1), cos(kron(w2<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
<span class="linenr"> 45: </span>A3 = [ones(length(w3),1), cos(kron(w3<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
<span class="linenr"> 46: </span>A4 = [ones(length(w4),1), cos(kron(w4<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
<span class="linenr"> 47: </span>
<span class="linenr"> 48: </span>B1 = [zeros(length(w1),1), sin(kron(w1<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
<span class="linenr"> 49: </span>B2 = [zeros(length(w2),1), sin(kron(w2<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
<span class="linenr"> 50: </span>B3 = [zeros(length(w3),1), sin(kron(w3<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
<span class="linenr"> 51: </span>B4 = [zeros(length(w4),1), sin(kron(w4<span class="org-builtin">'.*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>),[1<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))];
<span class="linenr"> 52: </span>
<span class="linenr"> 53: </span><span class="org-matlab-cellbreak">%% Convex optimization</span>
<span class="linenr"> 54: </span>cvx_begin
<span class="linenr"> 55: </span>
<span class="linenr"> 56: </span>variable y(n<span class="org-builtin">+</span>1,1)
<span class="linenr"> 57: </span>
<span class="linenr"> 58: </span><span class="org-comment-delimiter">% </span><span class="org-comment">t</span>
<span class="linenr"> 59: </span>maximize(<span class="org-builtin">-</span>y(1))
<span class="linenr"> 60: </span>
<span class="linenr"> 61: </span><span class="org-keyword">for</span> <span class="org-variable-name"><span class="org-matlab-math">i</span></span> = <span class="org-constant">1:length(w1)</span>
<span class="linenr"> 62: </span> norm([0 A1(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>); 0 B1(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>)]<span class="org-builtin">*</span>y) <span class="org-builtin"><=</span> 8e<span class="org-builtin">-</span>3;
<span class="linenr"> 63: </span><span class="org-keyword">end</span>
<span class="linenr"> 64: </span>
<span class="linenr"> 65: </span><span class="org-keyword">for</span> <span class="org-variable-name"><span class="org-matlab-math">i</span></span> = <span class="org-constant">1:length(w2)</span>
<span class="linenr"> 66: </span> norm([0 A2(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>); 0 B2(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>)]<span class="org-builtin">*</span>y) <span class="org-builtin"><=</span> 8e<span class="org-builtin">-</span>3<span class="org-builtin">*</span>(2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>w2(<span class="org-matlab-math">i</span>)<span class="org-builtin">/</span>(0.008<span class="org-builtin">*</span>2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>))<span class="org-builtin">^</span>3;
<span class="linenr"> 67: </span><span class="org-keyword">end</span>
<span class="linenr"> 68: </span>
<span class="linenr"> 69: </span><span class="org-keyword">for</span> <span class="org-variable-name"><span class="org-matlab-math">i</span></span> = <span class="org-constant">1:length(w3)</span>
<span class="linenr"> 70: </span> norm([0 A3(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>); 0 B3(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>)]<span class="org-builtin">*</span>y) <span class="org-builtin"><=</span> 3;
<span class="linenr"> 71: </span><span class="org-keyword">end</span>
<span class="linenr"> 72: </span>
<span class="linenr"> 73: </span><span class="org-keyword">for</span> <span class="org-variable-name"><span class="org-matlab-math">i</span></span> = <span class="org-constant">1:length(w4)</span>
<span class="linenr"> 74: </span> norm([[1 0]<span class="org-builtin">'-</span> [0 A4(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>); 0 B4(<span class="org-matlab-math">i</span>,<span class="org-builtin">:</span>)]<span class="org-builtin">*</span>y]) <span class="org-builtin"><=</span> y(1);
<span class="linenr"> 75: </span><span class="org-keyword">end</span>
<span class="linenr"> 76: </span>
<span class="linenr"> 77: </span>cvx_end
<span class="linenr"> 78: </span>
<span class="linenr"> 79: </span>h = y(2<span class="org-builtin">:</span>end);
<span class="linenr"> 80: </span>
<span class="linenr"> 81: </span><span class="org-matlab-cellbreak">%% Combine the frequency vectors to form the obtained filter</span>
<span class="linenr"> 82: </span>w = [w1 w2 w3 w4];
<span class="linenr"> 83: </span>H = [exp(<span class="org-builtin">-</span><span class="org-matlab-math">j</span><span class="org-builtin">*</span>kron(w<span class="org-builtin">'.*</span>2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span>,[0<span class="org-builtin">:</span>n<span class="org-builtin">-</span>1]))]<span class="org-builtin">*</span>h;
<span class="linenr"> 84: </span>
<span class="linenr"> 85: </span><span class="org-matlab-cellbreak">%% Bode plot of the obtained complementary filters</span>
<span class="linenr"> 86: </span><span class="org-builtin">figure</span>;
<span class="linenr"> 87: </span><span class="org-builtin">tiledlayout</span>(3, 1, <span class="org-string">'TileSpacing'</span>, <span class="org-string">'None'</span>, <span class="org-string">'Padding'</span>, <span class="org-string">'None'</span>);
<span class="linenr"> 88: </span>
<span class="linenr"> 89: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Magnitude</span>
<span class="linenr"> 90: </span>ax1 = <span class="org-builtin">nexttile</span>([2, 1]);
<span class="linenr"> 91: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr"> 92: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr"> 93: </span><span class="org-builtin">plot</span>(w, abs(1<span class="org-builtin">-</span>H), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$L_1$'</span>);
<span class="linenr"> 94: </span><span class="org-builtin">plot</span>([0.1, 10], [0.045, 0.045], <span class="org-string">'k:'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'Spec. on $L_1$'</span>);
<span class="linenr"> 95: </span>
<span class="linenr"> 96: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr"> 97: </span><span class="org-builtin">plot</span>(w, abs(H), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$H_1$'</span>);
<span class="linenr"> 98: </span><span class="org-builtin">plot</span>([0.0001, 0.008], [8e<span class="org-builtin">-</span>3, 8e<span class="org-builtin">-</span>3], <span class="org-string">'k--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'Spec. on $H_1$'</span>);
<span class="linenr"> 99: </span><span class="org-builtin">plot</span>([0.008 0.04], [8e<span class="org-builtin">-</span>3, 1], <span class="org-string">'k--'</span>, <span class="org-string">'HandleVisibility'</span>, <span class="org-string">'off'</span>);
<span class="linenr">100: </span><span class="org-builtin">plot</span>([0.04 0.1], [3, 3], <span class="org-string">'k--'</span>, <span class="org-string">'HandleVisibility'</span>, <span class="org-string">'off'</span>);
<span class="linenr">101: </span>
<span class="linenr">102: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>); <span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'YScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">103: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XTickLabel'</span>,[]); <span class="org-builtin">ylabel</span>(<span class="org-string">'Magnitude'</span>);
<span class="linenr">104: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr">105: </span><span class="org-builtin">ylim</span>([5e<span class="org-builtin">-</span>3, 10]);
<span class="linenr">106: </span>leg = <span class="org-builtin">legend</span>(<span class="org-string">'location'</span>, <span class="org-string">'southeast'</span>, <span class="org-string">'FontSize'</span>, 8, <span class="org-string">'NumColumns'</span>, 2);
<span class="linenr">107: </span>leg.ItemTokenSize(1) = 16;
<span class="linenr">108: </span>
<span class="linenr">109: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Phase</span>
<span class="linenr">110: </span>ax2 = <span class="org-builtin">nexttile</span>;
<span class="linenr">111: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr">112: </span><span class="org-builtin">plot</span>(w, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>unwrap(angle(1<span class="org-builtin">-</span>H)), <span class="org-string">'-'</span>);
<span class="linenr">113: </span><span class="org-builtin">plot</span>(w, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>unwrap(angle(H)), <span class="org-string">'-'</span>);
<span class="linenr">114: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr">115: </span><span class="org-builtin">xlabel</span>(<span class="org-string">'Frequency [Hz]'</span>); <span class="org-builtin">ylabel</span>(<span class="org-string">'Phase [deg]'</span>);
<span class="linenr">116: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">117: </span>yticks([<span class="org-builtin">-</span>360<span class="org-builtin">:</span>180<span class="org-builtin">:</span>180]); <span class="org-builtin">ylim</span>([<span class="org-builtin">-</span>380, 200]);
<span class="linenr">118: </span>
<span class="linenr">119: </span>linkaxes([ax1,ax2],<span class="org-string">'x'</span>);
<span class="linenr">120: </span><span class="org-builtin">xlim</span>([1e<span class="org-builtin">-</span>3, 1]);
<span class="linenr">121: </span>
<span class="linenr">122: </span><span class="org-matlab-cellbreak">%% Design of the weight for the high pass filter</span>
<span class="linenr">123: </span>w1 = 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>0.008; x1 = 0.35;
<span class="linenr">124: </span>w2 = 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>0.04; x2 = 0.5;
<span class="linenr">125: </span>w3 = 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>0.05; x3 = 0.5;
<span class="linenr">126: </span>
<span class="linenr">127: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Slope of +3 from w1</span>
<span class="linenr">128: </span>wH = 0.008<span class="org-builtin">*</span>(s<span class="org-builtin">^</span>2<span class="org-builtin">/</span>w1<span class="org-builtin">^</span>2 <span class="org-builtin">+</span> 2<span class="org-builtin">*</span>x1<span class="org-builtin">/</span>w1<span class="org-builtin">*</span>s <span class="org-builtin">+</span> 1)<span class="org-builtin">*</span>(s<span class="org-builtin">/</span>w1 <span class="org-builtin">+</span> 1);
<span class="linenr">129: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Little bump from w2 to w3</span>
<span class="linenr">130: </span>wH = wH<span class="org-builtin">*</span>(s<span class="org-builtin">^</span>2<span class="org-builtin">/</span>w2<span class="org-builtin">^</span>2 <span class="org-builtin">+</span> 2<span class="org-builtin">*</span>x2<span class="org-builtin">/</span>w2<span class="org-builtin">*</span>s <span class="org-builtin">+</span> 1)<span class="org-builtin">/</span>(s<span class="org-builtin">^</span>2<span class="org-builtin">/</span>w3<span class="org-builtin">^</span>2 <span class="org-builtin">+</span> 2<span class="org-builtin">*</span>x3<span class="org-builtin">/</span>w3<span class="org-builtin">*</span>s <span class="org-builtin">+</span> 1);
<span class="linenr">131: </span><span class="org-comment-delimiter">% </span><span class="org-comment">No Slope at high frequencies</span>
<span class="linenr">132: </span>wH = wH<span class="org-builtin">/</span>(s<span class="org-builtin">^</span>2<span class="org-builtin">/</span>w3<span class="org-builtin">^</span>2 <span class="org-builtin">+</span> 2<span class="org-builtin">*</span>x3<span class="org-builtin">/</span>w3<span class="org-builtin">*</span>s <span class="org-builtin">+</span> 1)<span class="org-builtin">/</span>(s<span class="org-builtin">/</span>w3 <span class="org-builtin">+</span> 1);
<span class="linenr">133: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Little bump between w2 and w3</span>
<span class="linenr">134: </span>w0 = 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>0.045; xi = 0.1; A = 2; n = 1;
<span class="linenr">135: </span>wH = wH<span class="org-builtin">*</span>((s<span class="org-builtin">^</span>2 <span class="org-builtin">+</span> 2<span class="org-builtin">*</span>w0<span class="org-builtin">*</span>xi<span class="org-builtin">*</span>A<span class="org-builtin">^</span>(1<span class="org-builtin">/</span>n)<span class="org-builtin">*</span>s <span class="org-builtin">+</span> w0<span class="org-builtin">^</span>2)<span class="org-builtin">/</span>(s<span class="org-builtin">^</span>2 <span class="org-builtin">+</span> 2<span class="org-builtin">*</span>w0<span class="org-builtin">*</span>xi<span class="org-builtin">*</span>s <span class="org-builtin">+</span> w0<span class="org-builtin">^</span>2))<span class="org-builtin">^</span>n;
<span class="linenr">136: </span>
<span class="linenr">137: </span>wH = 1<span class="org-builtin">/</span>wH;
<span class="linenr">138: </span>wH = minreal(ss(wH));
<span class="linenr">139: </span>
<span class="linenr">140: </span><span class="org-matlab-cellbreak">%% Design of the weight for the low pass filter</span>
<span class="linenr">141: </span>n = 20; <span class="org-comment-delimiter">% </span><span class="org-comment">Filter order</span>
<span class="linenr">142: </span>Rp = 1; <span class="org-comment-delimiter">% </span><span class="org-comment">Peak to peak passband ripple</span>
<span class="linenr">143: </span>Wp = 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>0.102; <span class="org-comment-delimiter">% </span><span class="org-comment">Edge frequency</span>
<span class="linenr">144: </span>
<span class="linenr">145: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Chebyshev Type I filter design</span>
<span class="linenr">146: </span>[b,a] = cheby1(n, Rp, Wp, <span class="org-string">'high'</span>, <span class="org-string">'s'</span>);
<span class="linenr">147: </span>wL = 0.04<span class="org-builtin">*</span>tf(a, b);
<span class="linenr">148: </span>
<span class="linenr">149: </span>wL = 1<span class="org-builtin">/</span>wL;
<span class="linenr">150: </span>wL = minreal(ss(wL));
<span class="linenr">151: </span>
<span class="linenr">152: </span><span class="org-matlab-cellbreak">%% Magnitude of the designed Weights and initial specifications</span>
<span class="linenr">153: </span><span class="org-builtin">figure</span>;
<span class="linenr">154: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr">155: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1);
<span class="linenr">156: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(inv(wL), freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_L|^{-1}$'</span>);
<span class="linenr">157: </span><span class="org-builtin">plot</span>([0.1, 10], [0.045, 0.045], <span class="org-string">'k:'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'Spec. on $L_1$'</span>);
<span class="linenr">158: </span>
<span class="linenr">159: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2);
<span class="linenr">160: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(inv(wH), freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_H|^{-1}$'</span>);
<span class="linenr">161: </span><span class="org-builtin">plot</span>([0.0001, 0.008], [8e<span class="org-builtin">-</span>3, 8e<span class="org-builtin">-</span>3], <span class="org-string">'k--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'Spec. on $H_1$'</span>);
<span class="linenr">162: </span><span class="org-builtin">plot</span>([0.008 0.04], [8e<span class="org-builtin">-</span>3, 1], <span class="org-string">'k--'</span>, <span class="org-string">'HandleVisibility'</span>, <span class="org-string">'off'</span>);
<span class="linenr">163: </span><span class="org-builtin">plot</span>([0.04 0.1], [3, 3], <span class="org-string">'k--'</span>, <span class="org-string">'HandleVisibility'</span>, <span class="org-string">'off'</span>);
<span class="linenr">164: </span>
<span class="linenr">165: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>); <span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'YScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">166: </span><span class="org-builtin">xlabel</span>(<span class="org-string">'Frequency [Hz]'</span>); <span class="org-builtin">ylabel</span>(<span class="org-string">'Magnitude'</span>);
<span class="linenr">167: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr">168: </span><span class="org-builtin">xlim</span>([freqs(1), freqs(end)]);
<span class="linenr">169: </span><span class="org-builtin">ylim</span>([5e<span class="org-builtin">-</span>3, 10]);
<span class="linenr">170: </span>leg = <span class="org-builtin">legend</span>(<span class="org-string">'location'</span>, <span class="org-string">'southeast'</span>, <span class="org-string">'FontSize'</span>, 8, <span class="org-string">'NumColumns'</span>, 2);
<span class="linenr">171: </span>leg.ItemTokenSize(1) = 16;
<span class="linenr">172: </span>
<span class="linenr">173: </span><span class="org-matlab-cellbreak">%% Generalized plant for the H-infinity Synthesis</span>
<span class="linenr">174: </span>P = [0 wL;
<span class="linenr">175: </span> wH <span class="org-builtin">-</span>wH;
<span class="linenr">176: </span> 1 0];
<span class="linenr">177: </span>
<span class="linenr">178: </span><span class="org-matlab-cellbreak">%% Standard H-Infinity synthesis</span>
<span class="linenr">179: </span>[Hl, <span class="org-builtin">~</span>, gamma, <span class="org-builtin">~</span>] = hinfsyn(P, 1, 1,<span class="org-string">'TOLGAM'</span>, 0.001, <span class="org-string">'METHOD'</span>, <span class="org-string">'ric'</span>, <span class="org-string">'DISPLAY'</span>, <span class="org-string">'on'</span>);
<span class="linenr">180: </span>
<span class="linenr">181: </span><span class="org-matlab-cellbreak">%% High pass filter as the complementary of the low pass filter</span>
<span class="linenr">182: </span>Hh = 1 <span class="org-builtin">-</span> Hl;
<span class="linenr">183: </span>
<span class="linenr">184: </span><span class="org-matlab-cellbreak">%% Minimum realization of the filters</span>
<span class="linenr">185: </span>Hh = minreal(Hh);
<span class="linenr">186: </span>Hl = minreal(Hl);
<span class="linenr">187: </span>
<span class="linenr">188: </span><span class="org-matlab-cellbreak">%% Bode plot of the obtained filters and comparison with the upper bounds</span>
<span class="linenr">189: </span><span class="org-builtin">figure</span>;
<span class="linenr">190: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr">191: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1);
<span class="linenr">192: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(Hl, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$L_1^\prime$'</span>);
<span class="linenr">193: </span><span class="org-builtin">plot</span>([0.1, 10], [0.045, 0.045], <span class="org-string">'k:'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'Spec. on $L_1$'</span>);
<span class="linenr">194: </span>
<span class="linenr">195: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2);
<span class="linenr">196: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(Hh, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$H_1^\prime$'</span>);
<span class="linenr">197: </span><span class="org-builtin">plot</span>([0.0001, 0.008], [8e<span class="org-builtin">-</span>3, 8e<span class="org-builtin">-</span>3], <span class="org-string">'k--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'Spec. on $H_1$'</span>);
<span class="linenr">198: </span><span class="org-builtin">plot</span>([0.008 0.04], [8e<span class="org-builtin">-</span>3, 1], <span class="org-string">'k--'</span>, <span class="org-string">'HandleVisibility'</span>, <span class="org-string">'off'</span>);
<span class="linenr">199: </span><span class="org-builtin">plot</span>([0.04 0.1], [3, 3], <span class="org-string">'k--'</span>, <span class="org-string">'HandleVisibility'</span>, <span class="org-string">'off'</span>);
<span class="linenr">200: </span>
<span class="linenr">201: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>); <span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'YScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">202: </span><span class="org-builtin">xlabel</span>(<span class="org-string">'Frequency [Hz]'</span>); <span class="org-builtin">ylabel</span>(<span class="org-string">'Magnitude'</span>);
<span class="linenr">203: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr">204: </span><span class="org-builtin">xlim</span>([freqs(1), freqs(end)]);
<span class="linenr">205: </span><span class="org-builtin">ylim</span>([5e<span class="org-builtin">-</span>3, 10]);
<span class="linenr">206: </span>leg = <span class="org-builtin">legend</span>(<span class="org-string">'location'</span>, <span class="org-string">'southeast'</span>, <span class="org-string">'FontSize'</span>, 8, <span class="org-string">'NumColumns'</span>, 2);
<span class="linenr">207: </span>leg.ItemTokenSize(1) = 16;
<span class="linenr">208: </span>
<span class="linenr">209: </span><span class="org-matlab-cellbreak">%% Comparison of the complementary filters obtained with H-infinity and with CVX</span>
<span class="linenr">210: </span><span class="org-builtin">figure</span>;
<span class="linenr">211: </span><span class="org-builtin">tiledlayout</span>(3, 1, <span class="org-string">'TileSpacing'</span>, <span class="org-string">'None'</span>, <span class="org-string">'Padding'</span>, <span class="org-string">'None'</span>);
<span class="linenr">212: </span>
<span class="linenr">213: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Magnitude</span>
<span class="linenr">214: </span>ax1 = <span class="org-builtin">nexttile</span>([2, 1]);
<span class="linenr">215: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr">216: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1);
<span class="linenr">217: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(Hl, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-comment">...</span>
<span class="linenr">218: </span> <span class="org-string">'DisplayName'</span>, <span class="org-string">'$L_1(s)$ - $\mathcal{H}_\infty$'</span>);
<span class="linenr">219: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2);
<span class="linenr">220: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(Hh, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-comment">...</span>
<span class="linenr">221: </span> <span class="org-string">'DisplayName'</span>, <span class="org-string">'$H_1(s)$ - $\mathcal{H}_\infty$'</span>);
<span class="linenr">222: </span>
<span class="linenr">223: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1);
<span class="linenr">224: </span><span class="org-builtin">plot</span>(w, abs(1<span class="org-builtin">-</span>H), <span class="org-string">'--'</span>, <span class="org-comment">...</span>
<span class="linenr">225: </span> <span class="org-string">'DisplayName'</span>, <span class="org-string">'$L_1(s)$ - FIR'</span>);
<span class="linenr">226: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2);
<span class="linenr">227: </span><span class="org-builtin">plot</span>(w, abs(H), <span class="org-string">'--'</span>, <span class="org-comment">...</span>
<span class="linenr">228: </span> <span class="org-string">'DisplayName'</span>, <span class="org-string">'$H_1(s)$ - FIR'</span>);
<span class="linenr">229: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr">230: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>); <span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'YScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">231: </span><span class="org-builtin">ylabel</span>(<span class="org-string">'Magnitude'</span>);
<span class="linenr">232: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XTickLabel'</span>,[]);
<span class="linenr">233: </span><span class="org-builtin">ylim</span>([5e<span class="org-builtin">-</span>3, 10]);
<span class="linenr">234: </span>leg = <span class="org-builtin">legend</span>(<span class="org-string">'location'</span>, <span class="org-string">'southeast'</span>, <span class="org-string">'FontSize'</span>, 8, <span class="org-string">'NumColumns'</span>, 2);
<span class="linenr">235: </span>leg.ItemTokenSize(1) = 16;
<span class="linenr">236: </span>
<span class="linenr">237: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Phase</span>
<span class="linenr">238: </span>ax2 = <span class="org-builtin">nexttile</span>;
<span class="linenr">239: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr">240: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1);
<span class="linenr">241: </span><span class="org-builtin">plot</span>(freqs, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>unwrap(angle(squeeze(freqresp(Hl, freqs, <span class="org-string">'Hz'</span>)))), <span class="org-string">'-'</span>);
<span class="linenr">242: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2);
<span class="linenr">243: </span><span class="org-builtin">plot</span>(freqs, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>unwrap(angle(squeeze(freqresp(Hh, freqs, <span class="org-string">'Hz'</span>)))), <span class="org-string">'-'</span>);
<span class="linenr">244: </span>
<span class="linenr">245: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1);
<span class="linenr">246: </span><span class="org-builtin">plot</span>(w, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>unwrap(angle(1<span class="org-builtin">-</span>H)), <span class="org-string">'--'</span>);
<span class="linenr">247: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2);
<span class="linenr">248: </span><span class="org-builtin">plot</span>(w, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>unwrap(angle(H)), <span class="org-string">'--'</span>);
<span class="linenr">249: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">250: </span><span class="org-builtin">xlabel</span>(<span class="org-string">'Frequency [Hz]'</span>); <span class="org-builtin">ylabel</span>(<span class="org-string">'Phase [deg]'</span>);
<span class="linenr">251: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr">252: </span>yticks([<span class="org-builtin">-</span>360<span class="org-builtin">:</span>180<span class="org-builtin">:</span>180]); <span class="org-builtin">ylim</span>([<span class="org-builtin">-</span>380, 200]);
<span class="linenr">253: </span>
<span class="linenr">254: </span>linkaxes([ax1,ax2],<span class="org-string">'x'</span>);
<span class="linenr">255: </span><span class="org-builtin">xlim</span>([freqs(1), freqs(end)]);
</pre>
</div>
</div>
</div>
<div id="outline-container-sec:3_closed_loop_complementary_filters" class="outline-3">
<h3 id="sec:3_closed_loop_complementary_filters"><span class="section-number-3">5.3.</span> <code>3_closed_loop_complementary_filters.m</code></h3>
<div class="outline-text-3" id="text-sec:3_closed_loop_complementary_filters">
<p>
This scripts corresponds to section 5.1 of (<a href="#citeproc_bib_item_1">Dehaeze, Vermat, and Collette 2021</a>).
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="linenr"> 1: </span><span class="org-matlab-cellbreak">%% Clear Workspace and Close figures</span>
<span class="linenr"> 2: </span>clear; close <span class="org-builtin">all</span>; clc;
<span class="linenr"> 3: </span>
<span class="linenr"> 4: </span><span class="org-matlab-cellbreak">%% Intialize Laplace variable</span>
<span class="linenr"> 5: </span>s = zpk(<span class="org-string">'s'</span>);
<span class="linenr"> 6: </span>
<span class="linenr"> 7: </span><span class="org-matlab-cellbreak">%% Initialize Frequency Vector</span>
<span class="linenr"> 8: </span>freqs = logspace(<span class="org-builtin">-</span>1, 3, 1000);
<span class="linenr"> 9: </span>
<span class="linenr">10: </span><span class="org-matlab-cellbreak">%% Design of the Weighting Functions</span>
<span class="linenr">11: </span>W1 = generateWF(<span class="org-string">'n'</span>, 3, <span class="org-string">'w0'</span>, 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>10, <span class="org-string">'G0'</span>, 1000, <span class="org-string">'Ginf'</span>, 1<span class="org-builtin">/</span>10, <span class="org-string">'Gc'</span>, 0.45);
<span class="linenr">12: </span>W2 = generateWF(<span class="org-string">'n'</span>, 2, <span class="org-string">'w0'</span>, 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>10, <span class="org-string">'G0'</span>, 1<span class="org-builtin">/</span>10, <span class="org-string">'Ginf'</span>, 1000, <span class="org-string">'Gc'</span>, 0.45);
<span class="linenr">13: </span>
<span class="linenr">14: </span><span class="org-matlab-cellbreak">%% Generalized plant for "closed-loop" complementary filter synthesis</span>
<span class="linenr">15: </span>P = [ W1 0 1;
<span class="linenr">16: </span> <span class="org-builtin">-</span>W1 W2 <span class="org-builtin">-</span>1];
<span class="linenr">17: </span>
<span class="linenr">18: </span><span class="org-matlab-cellbreak">%% Standard H-Infinity Synthesis</span>
<span class="linenr">19: </span>[L, <span class="org-builtin">~</span>, gamma, <span class="org-builtin">~</span>] = hinfsyn(P, 1, 1,<span class="org-string">'TOLGAM'</span>, 0.001, <span class="org-string">'METHOD'</span>, <span class="org-string">'ric'</span>, <span class="org-string">'DISPLAY'</span>, <span class="org-string">'on'</span>);
<span class="linenr">20: </span>
<span class="linenr">21: </span><span class="org-matlab-cellbreak">%% Complementary filters</span>
<span class="linenr">22: </span>H1 = inv(1 <span class="org-builtin">+</span> L);
<span class="linenr">23: </span>H2 = 1 <span class="org-builtin">-</span> H1;
<span class="linenr">24: </span>
<span class="linenr">25: </span><span class="org-matlab-cellbreak">%% Bode plot of the obtained Complementary filters with upper-bounds</span>
<span class="linenr">26: </span>freqs = logspace(<span class="org-builtin">-</span>1, 3, 1000);
<span class="linenr">27: </span><span class="org-builtin">figure</span>;
<span class="linenr">28: </span><span class="org-builtin">tiledlayout</span>(3, 1, <span class="org-string">'TileSpacing'</span>, <span class="org-string">'None'</span>, <span class="org-string">'Padding'</span>, <span class="org-string">'None'</span>);
<span class="linenr">29: </span>
<span class="linenr">30: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Magnitude</span>
<span class="linenr">31: </span>ax1 = <span class="org-builtin">nexttile</span>([2, 1]);
<span class="linenr">32: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr">33: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr">34: </span><span class="org-builtin">plot</span>(freqs, 1<span class="org-builtin">./</span>abs(squeeze(freqresp(W1, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_1|^{-1}$'</span>);
<span class="linenr">35: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr">36: </span><span class="org-builtin">plot</span>(freqs, 1<span class="org-builtin">./</span>abs(squeeze(freqresp(W2, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_2|^{-1}$'</span>);
<span class="linenr">37: </span>
<span class="linenr">38: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr">39: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(H1, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$H_1$'</span>);
<span class="linenr">40: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr">41: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(H2, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$H_2$'</span>);
<span class="linenr">42: </span>
<span class="linenr">43: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(L, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'k--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|L|$'</span>);
<span class="linenr">44: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr">45: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>); <span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'YScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">46: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XTickLabel'</span>,[]); <span class="org-builtin">ylabel</span>(<span class="org-string">'Magnitude'</span>);
<span class="linenr">47: </span><span class="org-builtin">ylim</span>([1e<span class="org-builtin">-</span>3, 1e3]);
<span class="linenr">48: </span>yticks([1e<span class="org-builtin">-</span>3, 1e<span class="org-builtin">-</span>2, 1e<span class="org-builtin">-</span>1, 1, 1e1, 1e2, 1e3]);
<span class="linenr">49: </span>yticklabels({<span class="org-string">''</span>, <span class="org-string">'$10^{-2}$'</span>, <span class="org-string">''</span>, <span class="org-string">'$10^0$'</span>, <span class="org-string">''</span>, <span class="org-string">'$10^2$'</span>, <span class="org-string">''</span>});
<span class="linenr">50: </span>leg = <span class="org-builtin">legend</span>(<span class="org-string">'location'</span>, <span class="org-string">'northeast'</span>, <span class="org-string">'FontSize'</span>, 8, <span class="org-string">'NumColumns'</span>, 3);
<span class="linenr">51: </span>leg.ItemTokenSize(1) = 18;
<span class="linenr">52: </span>
<span class="linenr">53: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Phase</span>
<span class="linenr">54: </span>ax2 = <span class="org-builtin">nexttile</span>;
<span class="linenr">55: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr">56: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr">57: </span><span class="org-builtin">plot</span>(freqs, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>phase(squeeze(freqresp(H1, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>);
<span class="linenr">58: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr">59: </span><span class="org-builtin">plot</span>(freqs, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>phase(squeeze(freqresp(H2, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>);
<span class="linenr">60: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr">61: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">62: </span><span class="org-builtin">xlabel</span>(<span class="org-string">'Frequency [Hz]'</span>); <span class="org-builtin">ylabel</span>(<span class="org-string">'Phase [deg]'</span>);
<span class="linenr">63: </span>yticks([<span class="org-builtin">-</span>180<span class="org-builtin">:</span>90<span class="org-builtin">:</span>180]);
<span class="linenr">64: </span><span class="org-builtin">ylim</span>([<span class="org-builtin">-</span>180, 200])
<span class="linenr">65: </span>yticklabels({<span class="org-string">'-180'</span>, <span class="org-string">''</span>, <span class="org-string">'0'</span>, <span class="org-string">''</span>, <span class="org-string">'180'</span>})
<span class="linenr">66: </span>
<span class="linenr">67: </span>linkaxes([ax1,ax2],<span class="org-string">'x'</span>);
<span class="linenr">68: </span><span class="org-builtin">xlim</span>([freqs(1), freqs(end)]);
</pre>
</div>
</div>
</div>
<div id="outline-container-sec:4_three_complementary_filters" class="outline-3">
<h3 id="sec:4_three_complementary_filters"><span class="section-number-3">5.4.</span> <code>4_three_complementary_filters.m</code></h3>
<div class="outline-text-3" id="text-sec:4_three_complementary_filters">
<p>
This scripts corresponds to section 5.2 of (<a href="#citeproc_bib_item_1">Dehaeze, Vermat, and Collette 2021</a>).
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="linenr"> 1: </span><span class="org-matlab-cellbreak">%% Clear Workspace and Close figures</span>
<span class="linenr"> 2: </span>clear; close <span class="org-builtin">all</span>; clc;
<span class="linenr"> 3: </span>
<span class="linenr"> 4: </span><span class="org-matlab-cellbreak">%% Intialize Laplace variable</span>
<span class="linenr"> 5: </span>s = zpk(<span class="org-string">'s'</span>);
<span class="linenr"> 6: </span>
<span class="linenr"> 7: </span>freqs = logspace(<span class="org-builtin">-</span>2, 3, 1000);
<span class="linenr"> 8: </span>
<span class="linenr"> 9: </span><span class="org-matlab-cellbreak">%% Design of the Weighting Functions</span>
<span class="linenr">10: </span>W1 = generateWF(<span class="org-string">'n'</span>, 2, <span class="org-string">'w0'</span>, 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>1, <span class="org-string">'G0'</span>, 1<span class="org-builtin">/</span>10, <span class="org-string">'Ginf'</span>, 1000, <span class="org-string">'Gc'</span>, 0.5);
<span class="linenr">11: </span>W2 = 0.22<span class="org-builtin">*</span>(1 <span class="org-builtin">+</span> s<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">/</span>1)<span class="org-builtin">^</span>2<span class="org-builtin">/</span>(sqrt(1e<span class="org-builtin">-</span>4) <span class="org-builtin">+</span> s<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">/</span>1)<span class="org-builtin">^</span>2<span class="org-builtin">*</span>(1 <span class="org-builtin">+</span> s<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">/</span>10)<span class="org-builtin">^</span>2<span class="org-builtin">/</span>(1 <span class="org-builtin">+</span> s<span class="org-builtin">/</span>2<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">/</span>1000)<span class="org-builtin">^</span>2;
<span class="linenr">12: </span>W3 = generateWF(<span class="org-string">'n'</span>, 3, <span class="org-string">'w0'</span>, 2<span class="org-builtin">*</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>10, <span class="org-string">'G0'</span>, 1000, <span class="org-string">'Ginf'</span>, 1<span class="org-builtin">/</span>10, <span class="org-string">'Gc'</span>, 0.5);
<span class="linenr">13: </span>
<span class="linenr">14: </span><span class="org-matlab-cellbreak">%% Inverse magnitude of the weighting functions</span>
<span class="linenr">15: </span><span class="org-builtin">figure</span>;
<span class="linenr">16: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr">17: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr">18: </span><span class="org-builtin">plot</span>(freqs, 1<span class="org-builtin">./</span>abs(squeeze(freqresp(W1, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_1|^{-1}$'</span>);
<span class="linenr">19: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr">20: </span><span class="org-builtin">plot</span>(freqs, 1<span class="org-builtin">./</span>abs(squeeze(freqresp(W2, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_2|^{-1}$'</span>);
<span class="linenr">21: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,3)
<span class="linenr">22: </span><span class="org-builtin">plot</span>(freqs, 1<span class="org-builtin">./</span>abs(squeeze(freqresp(W3, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_3|^{-1}$'</span>);
<span class="linenr">23: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>); <span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'YScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">24: </span><span class="org-builtin">xlabel</span>(<span class="org-string">'Frequency [Hz]'</span>); <span class="org-builtin">ylabel</span>(<span class="org-string">'Magnitude'</span>);
<span class="linenr">25: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr">26: </span><span class="org-builtin">xlim</span>([freqs(1), freqs(end)]); <span class="org-builtin">ylim</span>([2e<span class="org-builtin">-</span>4, 1.3e1])
<span class="linenr">27: </span>leg = <span class="org-builtin">legend</span>(<span class="org-string">'location'</span>, <span class="org-string">'northeast'</span>, <span class="org-string">'FontSize'</span>, 8);
<span class="linenr">28: </span>leg.ItemTokenSize(1) = 18;
<span class="linenr">29: </span>
<span class="linenr">30: </span><span class="org-matlab-cellbreak">%% Generalized plant for the synthesis of 3 complementary filters</span>
<span class="linenr">31: </span>P = [W1 <span class="org-builtin">-</span>W1 <span class="org-builtin">-</span>W1;
<span class="linenr">32: </span> 0 W2 0 ;
<span class="linenr">33: </span> 0 0 W3;
<span class="linenr">34: </span> 1 0 0];
<span class="linenr">35: </span>
<span class="linenr">36: </span><span class="org-matlab-cellbreak">%% Standard H-Infinity Synthesis</span>
<span class="linenr">37: </span>[H, <span class="org-builtin">~</span>, gamma, <span class="org-builtin">~</span>] = hinfsyn(P, 1, 2,<span class="org-string">'TOLGAM'</span>, 0.001, <span class="org-string">'METHOD'</span>, <span class="org-string">'ric'</span>, <span class="org-string">'DISPLAY'</span>, <span class="org-string">'on'</span>);
<span class="linenr">38: </span>
<span class="linenr">39: </span><span class="org-matlab-cellbreak">%% Synthesized H2 and H3 filters</span>
<span class="linenr">40: </span>H2 = tf(H(1));
<span class="linenr">41: </span>H3 = tf(H(2));
<span class="linenr">42: </span>
<span class="linenr">43: </span><span class="org-matlab-cellbreak">%% H1 is defined as the complementary filter of H2 and H3</span>
<span class="linenr">44: </span>H1 = 1 <span class="org-builtin">-</span> H2 <span class="org-builtin">-</span> H3;
<span class="linenr">45: </span>
<span class="linenr">46: </span><span class="org-matlab-cellbreak">%% Bode plot of the obtained complementary filters</span>
<span class="linenr">47: </span><span class="org-builtin">figure</span>;
<span class="linenr">48: </span><span class="org-builtin">tiledlayout</span>(3, 1, <span class="org-string">'TileSpacing'</span>, <span class="org-string">'None'</span>, <span class="org-string">'Padding'</span>, <span class="org-string">'None'</span>);
<span class="linenr">49: </span>
<span class="linenr">50: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Magnitude</span>
<span class="linenr">51: </span>ax1 = <span class="org-builtin">nexttile</span>([2, 1]);
<span class="linenr">52: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr">53: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr">54: </span><span class="org-builtin">plot</span>(freqs, 1<span class="org-builtin">./</span>abs(squeeze(freqresp(W1, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_1|^{-1}$'</span>);
<span class="linenr">55: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr">56: </span><span class="org-builtin">plot</span>(freqs, 1<span class="org-builtin">./</span>abs(squeeze(freqresp(W2, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_2|^{-1}$'</span>);
<span class="linenr">57: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,3)
<span class="linenr">58: </span><span class="org-builtin">plot</span>(freqs, 1<span class="org-builtin">./</span>abs(squeeze(freqresp(W3, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'--'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$|W_3|^{-1}$'</span>);
<span class="linenr">59: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr">60: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(H1, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$H_1$'</span>);
<span class="linenr">61: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr">62: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(H2, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$H_2$'</span>);
<span class="linenr">63: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,3)
<span class="linenr">64: </span><span class="org-builtin">plot</span>(freqs, abs(squeeze(freqresp(H3, freqs, <span class="org-string">'Hz'</span>))), <span class="org-string">'-'</span>, <span class="org-string">'DisplayName'</span>, <span class="org-string">'$H_3$'</span>);
<span class="linenr">65: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>); <span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'YScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">66: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr">67: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>); <span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'YScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">68: </span><span class="org-builtin">ylabel</span>(<span class="org-string">'Magnitude'</span>);
<span class="linenr">69: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XTickLabel'</span>,[]);
<span class="linenr">70: </span><span class="org-builtin">ylim</span>([1e<span class="org-builtin">-</span>4, 20]);
<span class="linenr">71: </span>leg = <span class="org-builtin">legend</span>(<span class="org-string">'location'</span>, <span class="org-string">'northeast'</span>, <span class="org-string">'FontSize'</span>, 8);
<span class="linenr">72: </span>leg.ItemTokenSize(1) = 18;
<span class="linenr">73: </span>
<span class="linenr">74: </span><span class="org-comment-delimiter">% </span><span class="org-comment">Phase</span>
<span class="linenr">75: </span>ax2 = <span class="org-builtin">nexttile</span>;
<span class="linenr">76: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">on;</span>
<span class="linenr">77: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,1)
<span class="linenr">78: </span><span class="org-builtin">plot</span>(freqs, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>phase(squeeze(freqresp(H1, freqs, <span class="org-string">'Hz'</span>))));
<span class="linenr">79: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,2)
<span class="linenr">80: </span><span class="org-builtin">plot</span>(freqs, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>phase(squeeze(freqresp(H2, freqs, <span class="org-string">'Hz'</span>))));
<span class="linenr">81: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>,<span class="org-string">'ColorOrderIndex'</span>,3)
<span class="linenr">82: </span><span class="org-builtin">plot</span>(freqs, 180<span class="org-builtin">/</span><span class="org-matlab-math">pi</span><span class="org-builtin">*</span>phase(squeeze(freqresp(H3, freqs, <span class="org-string">'Hz'</span>))));
<span class="linenr">83: </span><span class="org-builtin">hold</span> <span class="org-matlab-commanddual-string">off;</span>
<span class="linenr">84: </span><span class="org-builtin">xlabel</span>(<span class="org-string">'Frequency [Hz]'</span>); <span class="org-builtin">ylabel</span>(<span class="org-string">'Phase [deg]'</span>);
<span class="linenr">85: </span><span class="org-builtin">set</span>(<span class="org-variable-name">gca</span>, <span class="org-string">'XScale'</span>, <span class="org-string">'log'</span>);
<span class="linenr">86: </span>yticks([<span class="org-builtin">-</span>180<span class="org-builtin">:</span>90<span class="org-builtin">:</span>180]); <span class="org-builtin">ylim</span>([<span class="org-builtin">-</span>220, 220]);
<span class="linenr">87: </span>
<span class="linenr">88: </span>linkaxes([ax1,ax2],<span class="org-string">'x'</span>);
<span class="linenr">89: </span><span class="org-builtin">xlim</span>([freqs(1), freqs(end)]);
</pre>
</div>
</div>
</div>
<div id="outline-container-sec:generateWF" class="outline-3">
<h3 id="sec:generateWF"><span class="section-number-3">5.5.</span> <code>generateWF</code>: Generate Weighting Functions</h3>
<div class="outline-text-3" id="text-sec:generateWF">
<p>
This function is used to easily generate weighting functions from classical requirements.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">function</span> <span class="org-variable-name">[W]</span> = <span class="org-function-name">generateWF</span>(<span class="org-variable-name">args</span>)
<span class="org-comment-delimiter">% </span><span class="org-comment">createWeight -</span>
<span class="org-comment">%</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">Syntax: [W] = generateWeight(args)</span>
<span class="org-comment">%</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">Inputs:</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- n - Weight Order (integer)</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- G0 - Low frequency Gain</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- G1 - High frequency Gain</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- Gc - Gain of the weight at frequency w0</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- w0 - Frequency at which |W(j w0)| = Gc [rad/s]</span>
<span class="org-comment">%</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">Outputs:</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- W - Generated Weighting Function</span>
<span class="org-matlab-cellbreak">%% Argument validation</span>
<span class="org-keyword">arguments</span>
<span class="org-variable-name">args.n</span><span class="org-type"> (1,1) double</span> {mustBeInteger, mustBePositive} = 1
<span class="org-variable-name">args.G0</span><span class="org-type"> (1,1) double</span> {mustBeNumeric, mustBePositive} = 0.1
<span class="org-variable-name">args.Ginf</span><span class="org-type"> (1,1) double</span> {mustBeNumeric, mustBePositive} = 10
<span class="org-variable-name">args.Gc</span><span class="org-type"> (1,1) double</span> {mustBeNumeric, mustBePositive} = 1
<span class="org-variable-name">args.w0</span><span class="org-type"> (1,1) double</span> {mustBeNumeric, mustBePositive} = 1
<span class="org-keyword">end</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">Verification of correct relation between G0, Gc and Ginf</span>
mustBeBetween(args.G0, args.Gc, args.Ginf);
<span class="org-matlab-cellbreak">%% Initialize the Laplace variable</span>
s = zpk(<span class="org-string">'s'</span>);
<span class="org-matlab-cellbreak">%% Create the weighting function according to formula</span>
W = (((1<span class="org-builtin">/</span>args.w0)<span class="org-builtin">*</span>sqrt((1<span class="org-builtin">-</span>(args.G0<span class="org-builtin">/</span>args.Gc)<span class="org-builtin">^</span>(2<span class="org-builtin">/</span>args.n))<span class="org-builtin">/</span>(1<span class="org-builtin">-</span>(args.Gc<span class="org-builtin">/</span>args.Ginf)<span class="org-builtin">^</span>(2<span class="org-builtin">/</span>args.n)))<span class="org-builtin">*</span>s <span class="org-builtin">+</span> <span class="org-comment">...</span>
(args.G0<span class="org-builtin">/</span>args.Gc)<span class="org-builtin">^</span>(1<span class="org-builtin">/</span>args.n))<span class="org-builtin">/</span><span class="org-comment">...</span>
((1<span class="org-builtin">/</span>args.Ginf)<span class="org-builtin">^</span>(1<span class="org-builtin">/</span>args.n)<span class="org-builtin">*</span>(1<span class="org-builtin">/</span>args.w0)<span class="org-builtin">*</span>sqrt((1<span class="org-builtin">-</span>(args.G0<span class="org-builtin">/</span>args.Gc)<span class="org-builtin">^</span>(2<span class="org-builtin">/</span>args.n))<span class="org-builtin">/</span>(1<span class="org-builtin">-</span>(args.Gc<span class="org-builtin">/</span>args.Ginf)<span class="org-builtin">^</span>(2<span class="org-builtin">/</span>args.n)))<span class="org-builtin">*</span>s <span class="org-builtin">+</span> <span class="org-comment">...</span>
(1<span class="org-builtin">/</span>args.Gc)<span class="org-builtin">^</span>(1<span class="org-builtin">/</span>args.n)))<span class="org-builtin">^</span>args.n;
<span class="org-matlab-cellbreak">%% Custom validation function</span>
<span class="org-keyword">function</span> <span class="org-function-name">mustBeBetween</span>(<span class="org-variable-name">a</span>,<span class="org-variable-name">b</span>,<span class="org-variable-name">c</span>)
<span class="org-keyword">if</span> <span class="org-builtin">~</span>((a <span class="org-builtin">></span> b <span class="org-builtin">&&</span> b <span class="org-builtin">></span> c) <span class="org-builtin">||</span> (c <span class="org-builtin">></span> b <span class="org-builtin">&&</span> b <span class="org-builtin">></span> a))
eid = <span class="org-string">'createWeight:inputError'</span>;
msg = <span class="org-string">'Gc should be between G0 and Ginf.'</span>;
throwAsCaller(MException(eid,msg))
<span class="org-keyword">end</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-sec:generateCF" class="outline-3">
<h3 id="sec:generateCF"><span class="section-number-3">5.6.</span> <code>generateCF</code>: Generate Complementary Filters</h3>
<div class="outline-text-3" id="text-sec:generateCF">
<p>
This function is used to easily synthesize a set of two complementary filters using the \(\mathcal{H}_\infty\) synthesis.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">function</span> <span class="org-variable-name">[H1, H2]</span> = <span class="org-function-name">generateCF</span>(<span class="org-variable-name">W1</span>, <span class="org-variable-name">W2</span>, <span class="org-variable-name">args</span>)
<span class="org-comment-delimiter">% </span><span class="org-comment">createWeight -</span>
<span class="org-comment">%</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">Syntax: [H1, H2] = generateCF(W1, W2, args)</span>
<span class="org-comment">%</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">Inputs:</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- W1 - Weighting Function for H1</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- W2 - Weighting Function for H2</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- args:</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- method - H-Infinity solver ('lmi' or 'ric')</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- display - Display synthesis results ('on' or 'off')</span>
<span class="org-comment">%</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">Outputs:</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- H1 - Generated H1 Filter</span>
<span class="org-comment-delimiter">% </span><span class="org-comment">- H2 - Generated H2 Filter</span>
<span class="org-matlab-cellbreak">%% Argument validation</span>
<span class="org-keyword">arguments</span>
<span class="org-variable-name">W1</span>
<span class="org-variable-name">W2</span>
<span class="org-variable-name">args.method</span><span class="org-type"> char</span> {mustBeMember(args.method,{<span class="org-string">'lmi'</span>, <span class="org-string">'ric'</span>})} = <span class="org-string">'ric'</span>
<span class="org-variable-name">args.display</span><span class="org-type"> char</span> {mustBeMember(args.display,{<span class="org-string">'on'</span>, <span class="org-string">'off'</span>})} = <span class="org-string">'on'</span>
<span class="org-keyword">end</span>
<span class="org-matlab-cellbreak">%% The generalized plant is defined</span>
P = [W1 <span class="org-builtin">-</span>W1;
0 W2;
1 0];
<span class="org-matlab-cellbreak">%% The standard H-infinity synthesis is performed</span>
[H2, <span class="org-builtin">~</span>, gamma, <span class="org-builtin">~</span>] = hinfsyn(P, 1, 1,<span class="org-string">'TOLGAM'</span>, 0.001, <span class="org-string">'METHOD'</span>, args.method, <span class="org-string">'DISPLAY'</span>, args.display);
<span class="org-matlab-cellbreak">%% H1 is defined as the complementary of H2</span>
H1 = 1 <span class="org-builtin">-</span> H2;
</pre>
</div>
</div>
</div>
</div>
<style>.csl-entry{text-indent: -1.5em; margin-left: 1.5em;}</style><h2 class='citeproc-org-bib-h2'>Bibliography</h2>
<div class="csl-bib-body">
<div class="csl-entry"><a id="citeproc_bib_item_1"></a>Dehaeze, Thomas, Mohit Vermat, and Christophe Collette. 2021. “A New Method of Designing Complementary Filters for Sensor Fusion Using the H-Infinity Synthesis.” <i>Mechanical Systems and Signal Processing</i>, November.</div>
<div class="csl-entry"><a id="citeproc_bib_item_2"></a>Grant, Michael, and Stephen Boyd. 2014. “CVX: Matlab Software for Disciplined Convex Programming, Version 2.1.”</div>
<div class="csl-entry"><a id="citeproc_bib_item_3"></a>Hua, Wensheng, R Adhikari, Daniel B DeBra, Joseph A Giaime, Giles Dominic Hammond, C Hardham, Mike Hennessy, Jonathan P How, et al. 2004. “Low-Frequency Active Vibration Isolation for Advanced LIGO.” In <i>Gravitational Wave and Particle Astrophysics Detectors</i>, 5500:194–205. International Society for Optics and Photonics.</div>
<div class="csl-entry"><a id="citeproc_bib_item_4"></a>Hua, Wensheng, B. Debra, T. Hardham, T. Lantz, and A. Giaime. 2004. “Polyphase FIR Complementary Filters for Control Systems.” In <i>Proceedings of ASPE Spring Topical Meeting on Control of Precision Systems</i>, 109–14.</div>
<div class="csl-entry"><a id="citeproc_bib_item_5"></a>MATLAB. 2020. <i>Version 9.9.0 (R2020b)</i>. Natick, Massachusetts: The MathWorks Inc.</div>
<div class="csl-entry"><a id="citeproc_bib_item_6"></a>Sturm, Jos F. 1999. “Using SeDuMi 1.02, a Matlab Toolbox for Optimization over Symmetric Cones.” <i>Optimization Methods and Software</i> 11 (1-4). Taylor & Francis:625–53. <a href="https://doi.org/10.1080/10556789908805766">https://doi.org/10.1080/10556789908805766</a>.</div>
</div>
</div>
<div id="postamble" class="status">
<p class="author">Author: Dehaeze Thomas</p>
<p class="date">Created: 2021-09-02 jeu. 10:04</p>
</div>
</body>
</html>