Robust and Optimal Sensor Fusion - Tikz Figures
Table of Contents
- 1. Change some default
- 2. H-Infinity - Complementary filters - Generalized plant
- 3. H-Infinity - Complementary filters
- 4. H-Infinity - Optimal Complementary Filters
- 5. Fusion of two noisy sensors
- 6. Fusion of two noisy signals
- 7. Fusion of two noisy sensors with Dynamics
- 8. Fusion of two noisy sensors with Dynamics - Bis
- 9. Fusion of two sensors with mismatch dynamics
- 10. Uncertainty to Phase and Gain variation
- 11. Generate Complementary Filters using Feedback Control Architecture
- 12. H-Infinity Synthesis for Robust Sensor Fusion
- 13. Sensor fusion architecture with sensor dynamics uncertainty and noise
- 14. Equivalent super sensor
- 15. One sensor with noise
- 16. One sensor with normalized noise
- 17. One sensor with dynamic uncertainty
- 18. One sensor with dynamic uncertainty and noise
- 19. Huddle Test
Configuration file is accessible here.
1 Change some default
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}%
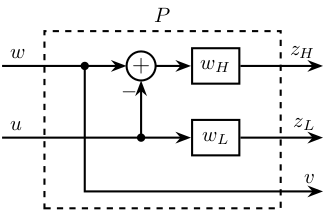
2 H-Infinity - Complementary filters - Generalized plant
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}% \begin{tikzpicture} \node[block={4.0cm}{3.0cm}, dashed] (P) {}; \node[above] at (P.north) {$P$}; \coordinate[] (inputw) at ($(P.south west)!0.8!(P.north west) + (-\cdist, 0)$); \coordinate[] (inputu) at ($(P.south west)!0.4!(P.north west) + (-\cdist, 0)$); \coordinate[] (outputh) at ($(P.south east)!0.8!(P.north east) + ( \cdist, 0)$); \coordinate[] (outputl) at ($(P.south east)!0.4!(P.north east) + ( \cdist, 0)$); \coordinate[] (outputv) at ($(P.south east)!0.1!(P.north east) + ( \cdist, 0)$); \node[block, left=2*\cdist of outputl] (WL){$w_L$}; \node[block, left=2*\cdist of outputh] (WH){$w_H$}; \node[addb={+}{}{}{}{-}, left=of WH] (sub) {}; \draw[->] (inputw) node[above right]{$w$} -- (sub.west); \draw[->] (inputu) node[above right]{$u$} -- (WL.west); \draw[->] (inputu-|sub) node[branch]{} -- (sub.south); \draw[->] (sub.east) -- (WH.west); \draw[->] ($(inputw)+(2*\cdist, 0)$) node[branch]{} |- (outputv) node[above left]{$v$}; \draw[->] (WH.east) -- (outputh)node[above left]{$z_H$}; \draw[->] (WL.east) -- (outputl)node[above left]{$z_L$}; \end{tikzpicture}
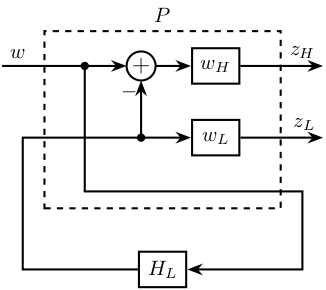
3 H-Infinity - Complementary filters
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}% \begin{tikzpicture} \node[block={4.0cm}{3.0cm}, dashed] (P) {}; \node[above] at (P.north) {$P$}; \coordinate[] (inputw) at ($(P.south west)!0.8!(P.north west) + (-\cdist, 0)$); \coordinate[] (inputu) at ($(P.south west)!0.4!(P.north west) + (-\cdist, 0)$); \coordinate[] (outputh) at ($(P.south east)!0.8!(P.north east) + ( \cdist, 0)$); \coordinate[] (outputl) at ($(P.south east)!0.4!(P.north east) + ( \cdist, 0)$); \coordinate[] (outputv) at ($(P.south east)!0.1!(P.north east) + ( \cdist, 0)$); \node[block, left=2*\cdist of outputl] (WL){$w_L$}; \node[block, left=2*\cdist of outputh] (WH){$w_H$}; \node[addb={+}{}{}{}{-}, left=of WH] (sub) {}; \node[block, below=\cdist of P] (HL) {$H_L$}; \draw[->] (inputw) node[above right]{$w$} -- (sub.west); \draw[->] (HL.west) -| ($(inputu)+(0.5*\cdist, 0)$) -- (WL.west); \draw[->] (inputu-|sub) node[branch]{} -- (sub.south); \draw[->] (sub.east) -- (WH.west); \draw[->] ($(inputw)+(2*\cdist, 0)$) node[branch]{} |- ($(outputv)+(-0.5*\cdist, 0)$) |- (HL.east); \draw[->] (WH.east) -- (outputh)node[above left]{$z_H$}; \draw[->] (WL.east) -- (outputl)node[above left]{$z_L$}; \end{tikzpicture}
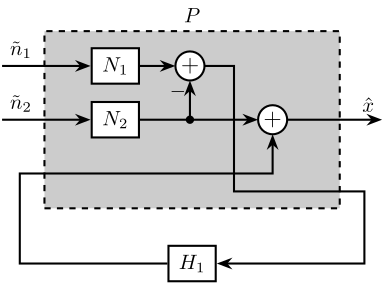
4 H-Infinity - Optimal Complementary Filters
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}% \begin{tikzpicture} \node[block={5.0cm}{3.0cm}, dashed] (P) {}; \node[above] at (P.north) {$P$}; \coordinate[] (inputn1) at ($(P.south west)!0.8!(P.north west) + (-\cdist, 0)$); \coordinate[] (inputn2) at ($(P.south west)!0.5!(P.north west) + (-\cdist, 0)$); \coordinate[] (inputu) at ($(P.south west)!0.2!(P.north west) + (-\cdist, 0)$); \coordinate[] (outputx) at ($(P.south east)!0.5!(P.north east) + ( \cdist, 0)$); \coordinate[] (outputv) at ($(P.south east)!0.1!(P.north east) + ( \cdist, 0)$); \node[block, right=1.5 of inputn1] (W1){$W_1$}; \node[block, right=1.5 of inputn2] (W2){$W_2$}; \node[addb={+}{}{}{}{-}, right=of W1] (sub) {}; \node[addb, right=2 of W2] (add) {}; \node[block, below=of P] (H1) {$H_1$}; \draw[->] (inputn1)node[above right]{$n_1$} -- (W1.west); \draw[->] (inputn2)node[above right]{$n_2$} -- (W2.west); \draw[->] (W1) -- (sub.west); \draw[->] (W2) -| (sub.south); \draw[->] (W2-|sub.south) node[branch]{} -- (add.west); \draw[->] (sub.east) -- ++(0.5, 0) |- ($(outputv) + (-0.3, 0)$) |- (H1.east); \draw[->] (H1.west) -| ($(inputu) + (0.3, 0)$) -| (add.south); \draw[->] (add.east) -- (outputx) node[above left]{$\hat{x}$}; \end{tikzpicture}
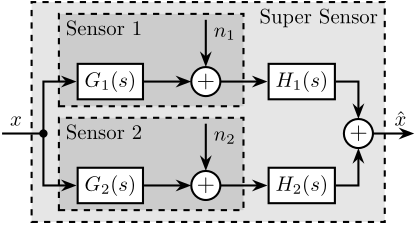
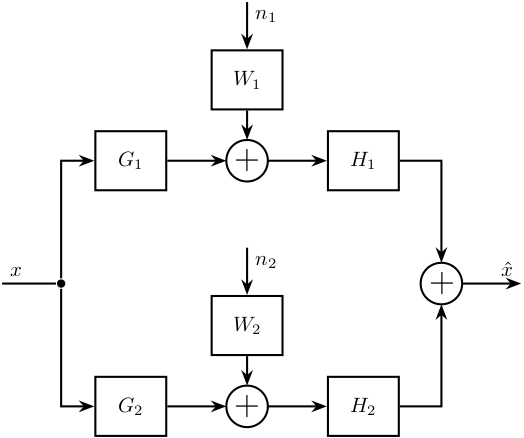
5 Fusion of two noisy sensors
\begin{tikzpicture} \node[branch] (x) at (0, 0); \node[addb, above right=1.5 and 1 of x](add1){}; \node[addb, below right=1.5 and 1 of x](add2){}; \node[block, above=0.5 of add1](W1){$W_1$}; \node[block, above=0.5 of add2](W2){$W_2$}; \node[block, right=1 of add1](H1){$H_1$}; \node[block, right=1 of add2](H2){$H_2$}; \node[addb, right=4 of x](add){}; \draw[] ($(x)+(-1, 0)$) node[above right]{$x$} -- (x); \draw[->] (x) |- (add1.west); \draw[->] (x) |- (add2.west); \draw[->] (W1.south) -- (add1.north); \draw[->] (W2.south) -- (add2.north); \draw[<-] (W1.north) -- ++(0, 0.8)node[below right]{$n_1$}; \draw[<-] (W2.north) -- ++(0, 0.8)node[below right]{$n_2$}; \draw[->] (add1.east) -- (H1.west); \draw[->] (add2.east) -- (H2.west); \draw[->] (H1) -| (add.north); \draw[->] (H2) -| (add.south); \draw[->] (add.east) -- ++(1, 0) node[above left]{$\hat{x}$}; \end{tikzpicture}
6 Fusion of two noisy signals
\begin{tikzpicture} \node[addb] (add) at (0, 0){}; \node[block, above left=0.5 and 0.8 of add] (H1) {$H_1$}; \node[block, below left=0.5 and 0.8 of add] (H2) {$H_2$}; \draw[->] ($(H1.west)+(-1.5, 0)$)node[above right]{$x + n_1$} -- (H1.west); \draw[->] ($(H2.west)+(-1.5, 0)$)node[above right]{$x + n_2$} -- (H2.west); \draw[->] (H1) -| (add.north); \draw[->] (H2) -| (add.south); \draw[->] (add.east) -- ++(1, 0) node[above left]{$\hat{x}$}; \end{tikzpicture}
7 Fusion of two noisy sensors with Dynamics
\begin{tikzpicture} \node[branch] (x) at (0, 0); \node[block, above right=1.5 and 0.5 of x](G1){$G_1$}; \node[block, below right=1.5 and 0.5 of x](G2){$G_2$}; \node[addb, right=1 of G1](add1){}; \node[addb, right=1 of G2](add2){}; \node[block, above=0.5 of add1](W1){$W_1$}; \node[block, above=0.5 of add2](W2){$W_2$}; \node[block, right=1 of add1](H1){$H_1$}; \node[block, right=1 of add2](H2){$H_2$}; \node[addb, right=6 of x](add){}; \draw[] ($(x)+(-1, 0)$) node[above right]{$x$} -- (x); \draw[->] (x) |- (G1.west); \draw[->] (x) |- (G2.west); \draw[->] (G1.east) -- (add1.west); \draw[->] (G2.east) -- (add2.west); \draw[->] (W1.south) -- (add1.north); \draw[->] (W2.south) -- (add2.north); \draw[<-] (W1.north) -- ++(0, 0.8)node[below right]{$n_1$}; \draw[<-] (W2.north) -- ++(0, 0.8)node[below right]{$n_2$}; \draw[->] (add1.east) -- (H1.west); \draw[->] (add2.east) -- (H2.west); \draw[->] (H1) -| (add.north); \draw[->] (H2) -| (add.south); \draw[->] (add.east) -- ++(1, 0) node[above left]{$\hat{x}$}; \end{tikzpicture}
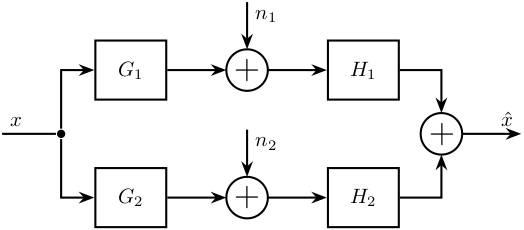
8 Fusion of two noisy sensors with Dynamics - Bis
\begin{tikzpicture} \node[branch] (x) at (0, 0); \node[block, above right=0.5 and 0.5 of x](G1){$G_1$}; \node[block, below right=0.5 and 0.5 of x](G2){$G_2$}; \node[addb, right=1 of G1](add1){}; \node[addb, right=1 of G2](add2){}; \node[block, right=1 of add1](H1){$H_1$}; \node[block, right=1 of add2](H2){$H_2$}; \node[addb, right=6 of x](add){}; \draw[] ($(x)+(-1, 0)$) node[above right]{$x$} -- (x); \draw[->] (x) |- (G1.west); \draw[->] (x) |- (G2.west); \draw[->] (G1.east) -- (add1.west); \draw[->] (G2.east) -- (add2.west); \draw[<-] (add1.north) -- ++(0, 0.8)node[below right]{$n_1$}; \draw[<-] (add2.north) -- ++(0, 0.8)node[below right]{$n_2$}; \draw[->] (add1.east) -- (H1.west); \draw[->] (add2.east) -- (H2.west); \draw[->] (H1) -| (add.north); \draw[->] (H2) -| (add.south); \draw[->] (add.east) -- ++(1, 0) node[above left]{$\hat{x}$}; \end{tikzpicture}
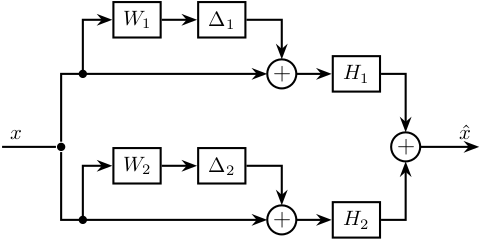
9 Fusion of two sensors with mismatch dynamics
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}% \begin{tikzpicture} \node[branch] (x) at (0, 0); \node[addb, above right=1 and 3.5 of x](add1){}; \node[addb, below right=1 and 3.5 of x](add2){}; \node[block, above left= of add1](delta1){$\Delta_1$}; \node[block, above left= of add2](delta2){$\Delta_2$}; \node[block, left= of delta1](W1){$W_1$}; \node[block, left= of delta2](W2){$W_2$}; \node[block, right= of add1](H1){$H_1$}; \node[block, right= of add2](H2){$H_2$}; \node[addb, right=5.5 of x](add){}; \draw[] ($(x)+(-1, 0)$) node[above right]{$x$} -- (x); \draw[->] (x) |- (add1.west); \draw[->] (x) |- (add2.west); \draw[->] ($(add1-|W1.west)+(-0.5, 0)$)node[branch]{} |- (W1.west); \draw[->] ($(add2-|W2.west)+(-0.5, 0)$)node[branch]{} |- (W2.west); \draw[->] (W1.east) -- (delta1.west); \draw[->] (W2.east) -- (delta2.west); \draw[->] (delta1.east) -| (add1.north); \draw[->] (delta2.east) -| (add2.north); \draw[->] (add1.east) -- (H1.west); \draw[->] (add2.east) -- (H2.west); \draw[->] (H1.east) -| (add.north); \draw[->] (H2.east) -| (add.south); \draw[->] (add.east) -- ++(1, 0) node[above left]{$\hat{x}$}; \end{tikzpicture}
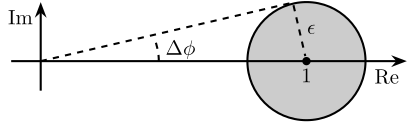
10 Uncertainty to Phase and Gain variation
\begin{tikzpicture} \draw[->] (-0.5, 0) -- (7, 0) node[below left]{Real}; \draw[->] (0, -1) -- (0, 1) node[left]{Im}; \node[branch] (1) at (5, 0){}; \node[below] at (1){$1$}; \node[circle, draw] (c) at (1)[minimum size=2cm]{}; \draw[dashed] (0, 0) -- (tangent cs:node=c,point={(0, 0)},solution=2) -- node[midway, right]{$|H_i W_i|$} (1); \draw[dashed] (2, 0) arc (0:23:1) node[midway, right]{$\Delta \phi$}; % \draw[dashed] (0, 0) -- (tangent cs:node=c,point={(0, 0)},solution=1) coordinate(cbot); \end{tikzpicture}
11 Generate Complementary Filters using Feedback Control Architecture
\begin{tikzpicture} \node[addb={+}{}{}{}{-}] (addfb) at (0, 0){}; \node[block, right=1 of addfb] (L){$L$}; \node[addb={+}{}{}{}{}, right=1 of L] (adddy){}; \draw[<-] (addfb.west) -- ++(-1, 0) node[above right]{$y_1$}; \draw[->] (addfb.east) -- (L.west); \draw[->] (L.east) -- (adddy.west); \draw[->] (adddy.east) -- ++(1, 0) node[above left]{$y_s$}; \draw[->] ($(adddy.east) + (0.5, 0)$) node[branch]{} -- ++(0, -1) -| (addfb.south); \draw[<-] (adddy.north) -- ++(0, 1) node[below right]{$y_2$}; \end{tikzpicture}
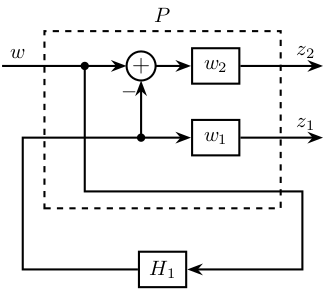
12 H-Infinity Synthesis for Robust Sensor Fusion
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}% \begin{tikzpicture} \node[block={4.0cm}{3.0cm}, dashed] (P) {}; \node[above] at (P.north) {$P$}; \coordinate[] (inputw) at ($(P.south west)!0.8!(P.north west) + (-\cdist, 0)$); \coordinate[] (inputu) at ($(P.south west)!0.4!(P.north west) + (-\cdist, 0)$); \coordinate[] (outputh) at ($(P.south east)!0.8!(P.north east) + ( \cdist, 0)$); \coordinate[] (outputl) at ($(P.south east)!0.4!(P.north east) + ( \cdist, 0)$); \coordinate[] (outputv) at ($(P.south east)!0.1!(P.north east) + ( \cdist, 0)$); \node[block, left=2*\cdist of outputl] (W1){$w_1$}; \node[block, left=2*\cdist of outputh] (W2){$w_2$}; \node[addb={+}{}{}{}{-}, left=of W2] (sub) {}; \node[block, below=\cdist of P] (H1) {$H_1$}; \draw[->] (inputw) node[above right]{$w$} -- (sub.west); \draw[->] (H1.west) -| ($(inputu)+(0.5*\cdist, 0)$) -- (W1.west); \draw[->] (inputu-|sub) node[branch]{} -- (sub.south); \draw[->] (sub.east) -- (W2.west); \draw[->] ($(inputw)+(2*\cdist, 0)$) node[branch]{} |- ($(outputv)+(-0.5*\cdist, 0)$) |- (H1.east); \draw[->] (W2.east) -- (outputh)node[above left]{$z_2$}; \draw[->] (W1.east) -- (outputl)node[above left]{$z_1$}; \end{tikzpicture}
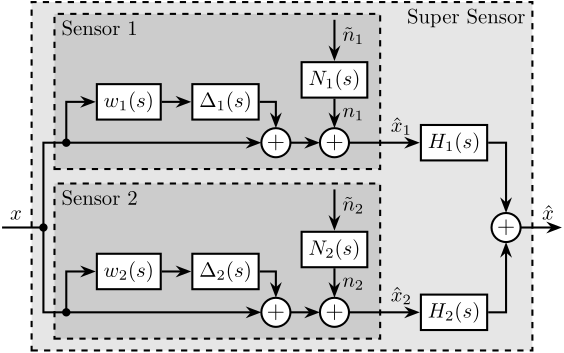
13 Sensor fusion architecture with sensor dynamics uncertainty and noise
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}% \begin{tikzpicture} \node[branch] (x) at (0, 0); \node[addb, above right=1.2 and 3.7 of x](add1){}; \node[addb, below right=1.2 and 3.7 of x](add2){}; \node[block, above left=0.2 and 0.1 of add1](delta1){$\Delta_1(s)$}; \node[block, above left=0.2 and 0.1 of add2](delta2){$\Delta_2(s)$}; \node[block, left=0.5 of delta1](W1){$w_1(s)$}; \node[block, left=0.5 of delta2](W2){$w_2(s)$}; \node[addb, right=0.5 of add1](addn1){}; \node[addb, right=0.5 of add2](addn2){}; \node[block, above=0.5 of addn1](N1) {$N_1(s)$}; \node[block, above=0.5 of addn2](N2) {$N_2(s)$}; \node[block, right=1.2 of addn1](H1){$H_1(s)$}; \node[block, right=1.2 of addn2](H2){$H_2(s)$}; \node[addb, right=7.5 of x](add){}; \draw[] ($(x)+(-0.7, 0)$) node[above right]{$x$} -- (x.center); \draw[->] (x.center) |- (add1.west); \draw[->] (x.center) |- (add2.west); \draw[->] ($(add1-|W1.west)+(-0.5, 0)$)node[branch](S1){} |- (W1.west); \draw[->] ($(add2-|W2.west)+(-0.5, 0)$)node[branch](S2){} |- (W2.west); \draw[->] (W1.east) -- (delta1.west); \draw[->] (W2.east) -- (delta2.west); \draw[->] (delta1.east) -| (add1.north); \draw[->] (delta2.east) -| (add2.north); \draw[->] (add1.east) -- (addn1.west); \draw[->] (add2.east) -- (addn2.west); \draw[->] (addn1.east) -- (H1.west)node[above left]{$\hat{x}_1$}; \draw[->] (addn2.east) -- (H2.west)node[above left]{$\hat{x}_2$}; \draw[->] ($(N1.north)+(0,0.7)$) node[below right](n1){$\tilde{n}_1$} -- (N1.north); \draw[->] ($(N2.north)+(0,0.7)$) node[below right](n2){$\tilde{n}_2$} -- (N2.north); \draw[->] (N1.south) -- (addn1.north)node[above right]{$n_1$}; \draw[->] (N2.south) -- (addn2.north)node[above right]{$n_2$}; \draw[->] (H1.east) -| (add.north); \draw[->] (H2.east) -| (add.south); \draw[->] (add.east) -- ++(0.7, 0) node[above left]{$\hat{x}$}; \begin{scope}[on background layer] \node[fit={($(add2.south-|x)+(-0.2, -0.4)$) ($(n1.north-|add.east)+(0.2, 0.3)$)}, fill=black!10!white, draw, dashed, inner sep=0pt] (supersensor) {}; \node[below left] at (supersensor.north east) {Super Sensor}; \node[block, fit={($(S1|-add1.south)+(-0.2, -0.2)$) ($(n1.north-|N1.east)+(0.2, 0.1)$)}, fill=black!20!white, dashed, inner sep=0pt] (sensor1) {}; \node[below right] at (sensor1.north west) {Sensor 1}; \node[block, fit={($(S2|-add2.south)+(-0.2, -0.2)$) ($(n2.north-|N2.east)+(0.2, 0.1)$)}, fill=black!20!white, dashed, inner sep=0pt] (sensor2) {}; \node[below right] at (sensor2.north west) {Sensor 2}; \end{scope} \end{tikzpicture}
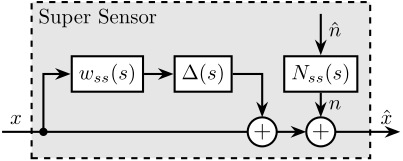
14 Equivalent super sensor
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}% \begin{tikzpicture} \node[branch] (x) at (0, 0); \node[block, above right=0.6 and 0.4 of x](Wss){$w_{ss}(s)$}; \node[block, right=0.5 of Wss](delta){$\Delta(s)$}; \node[addb](add) at ($(delta.east|-x) + (0.5, 0)$){}; \node[addb, right=0.5 of add](addn){}; \node[block](Nss) at (delta-|addn) {$N_{ss}(s)$}; \draw[] ($(x)+(-0.7, 0)$) node[above right]{$x$} -- (add.west); \draw[->] (x.center) |- (Wss); \draw[->] (Wss.east) -- (delta.west); \draw[->] (delta.east) -| (add.north); \draw[->] (add.east) -- (addn.west); \draw[->] ($(Nss.north)+(0,0.7)$) node[below right](nss){$\hat{n}$} -- (Nss.north); \draw[->] (Nss.south) -- (addn.north) node[above right]{$n$}; \draw[->] (addn.east) -- ++(1.1, 0) node[above left]{$\hat{x}$}; \begin{scope}[on background layer] \node[fit={($(add.south-|x)+(-0.2, -0.2)$) ($(Nss.east|-nss.north)+(0.2, 0.2)$)}, fill=black!10!white, draw, dashed, inner sep=0pt] (supersensor) {}; \node[below right] at (supersensor.north west) {Super Sensor}; \end{scope} \end{tikzpicture}
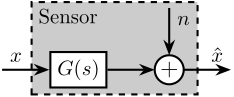
15 One sensor with noise
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}% \begin{tikzpicture} \node[block] (G) at (0, 0) {$G(s)$}; \node[addb, right=0.8 of G] (add) {}; \draw[->] ($(G.west) + (-0.8, 0)$)node[above right]{$x$} -- (G.west); \draw[->] (G.east) -- (add.west); \draw[->] ($(add.north) + (0, 0.8)$)node[below right](n){$n$} -- (add.north); \draw[->] (add.east) -- ++(0.8, 0) node[above left]{$\hat{x}$}; \begin{scope}[on background layer] \node[fit={($(G.south west)+(-0.3, -0.1)$) ($(n.north east)+(0.0, 0.1)$)}, fill=black!20!white, draw, dashed, inner sep=0pt] (sensor) {}; \node[below right] at (sensor.north west) {Sensor}; \end{scope} \end{tikzpicture}
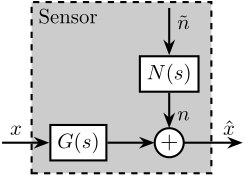
16 One sensor with normalized noise
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}% \begin{tikzpicture} \node[block] (G) at (0, 0) {$G(s)$}; \node[addb, right=0.8 of G] (add) {}; \node[block, above=0.6 of add] (N) {$N(s)$}; \draw[->] ($(G.west) + (-0.8, 0)$)node[above right]{$x$} -- (G.west); \draw[->] (G.east) -- (add.west); \draw[->] ($(N.north) + (0, 0.8)$)node[below right](ntilde){$\tilde{n}$} -- (N.north); \draw[->] (N.south) -- (add.north)node[above right](n){$n$}; \draw[->] (add.east) -- ++(1.0, 0) node[above left]{$\hat{x}$}; \begin{scope}[on background layer] \node[fit={($(G.south west)+(-0.3, -0.2)$) ($(ntilde.north-|N.east)+(0.2, 0.1)$)}, fill=black!20!white, draw, dashed, inner sep=0pt] (sensor) {}; \node[below right] at (sensor.north west) {Sensor}; \end{scope} \end{tikzpicture}
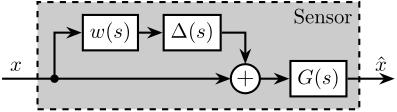
17 One sensor with dynamic uncertainty
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}% \begin{tikzpicture} \node[branch] (x) at (0, 0) {}; \node[block, above right=0.4 and 0.4 of x](W){$w(s)$}; \node[block, right=0.4 of W](delta){$\Delta(s)$}; \node[addb](add) at ($(delta.east|-x) + (0.4, 0)$) {}; \node[block, right=0.5 of add](G){$G(s)$}; \draw[->] ($(x.west) + (-0.8, 0)$)node[above right]{$x$} -- (add.west); \draw[->] (x.center) |- (W.west); \draw[->] (W.east) -- (delta.west); \draw[->] (delta.east) -| (add.north); \draw[->] (add.east) -- (G.west); \draw[->] (G.east) -- ++(0.8, 0) node[above left]{$\hat{x}$}; \begin{scope}[on background layer] \node[fit={($(x.west|-G.south)+(-0.2, -0.2)$) ($(delta.north-|G.east)+(0.2, 0.2)$)}, fill=black!20!white, draw, dashed, inner sep=0pt] (sensor) {}; \node[below left] at (sensor.north east) {Sensor}; \end{scope} \end{tikzpicture}
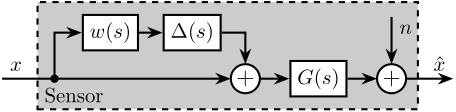
18 One sensor with dynamic uncertainty and noise
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}% \begin{tikzpicture} \node[branch] (x) at (0, 0) {}; \node[block, above right=0.4 and 0.4 of x](W){$w(s)$}; \node[block, right=0.4 of W](delta){$\Delta(s)$}; \node[addb](add) at ($(delta.east|-x) + (0.4, 0)$) {}; \node[block, right=0.5 of add](G){$G(s)$}; \node[addb, right=0.5 of G] (addn) {}; \draw[->] ($(x.west) + (-0.8, 0)$)node[above right]{$x$} -- (add.west); \draw[->] (x.center) |- (W.west); \draw[->] (W.east) -- (delta.west); \draw[->] (delta.east) -| (add.north); \draw[->] (add.east) -- (G.west); \draw[->] (G.east) -- (addn.west); \draw[->] ($(addn.north)+(0, 0.8)$) node[below right]{$n$} -- (addn.north); \draw[->] (addn.east) -- ++(0.8, 0) node[above left]{$\hat{x}$}; \begin{scope}[on background layer] \node[fit={($(x.west|-G.south)+(-0.2, -0.2)$) ($(delta.north-|addn.east)+(0.2, 0.2)$)}, fill=black!20!white, draw, dashed, inner sep=0pt] (sensor) {}; \node[above right] at (sensor.south west) {Sensor}; \end{scope} \end{tikzpicture}
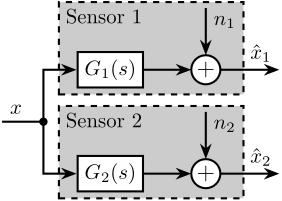
19 Huddle Test
\tikzset{block/.default={0.8cm}{0.6cm}} \tikzset{addb/.append style={scale=0.7}} \tikzset{node distance=0.6} \def\cdist{0.7} \definecolor{T}{rgb}{0.230, 0.299, 0.754}% \definecolor{S}{rgb}{0.706, 0.016, 0.150}% \begin{tikzpicture} \node[branch] (x) at (0, 0); \node[block, above right=0.5 and 0.5 of x](G1){$G_1(s)$}; \node[block, below right=0.5 and 0.5 of x](G2){$G_2(s)$}; \node[addb, right=0.8 of G1](add1){}; \node[addb, right=0.8 of G2](add2){}; \draw[] ($(x)+(-0.7, 0)$) node[above right]{$x$} -- (x.center); \draw[->] (x.center) |- (G1.west); \draw[->] (x.center) |- (G2.west); \draw[->] (G1.east) -- (add1.west); \draw[->] (G2.east) -- (add2.west); \draw[<-] (add1.north) -- ++(0, 0.8)node[below right](n1){$n_1$}; \draw[<-] (add2.north) -- ++(0, 0.8)node[below right](n2){$n_2$}; \draw[->] (add1.east) -- ++(1, 0)node[above left]{$\hat{x}_1$}; \draw[->] (add2.east) -- ++(1, 0)node[above left]{$\hat{x}_2$}; \begin{scope}[on background layer] % \node[fit={($(G2.south-|x)+(-0.2, -0.3)$) ($(n1.north east-|add.east)+(0.2, 0.3)$)}, fill=black!10!white, draw, dashed, inner sep=0pt] (supersensor) {}; % \node[below left] at (supersensor.north east) {Super Sensor}; \node[fit={($(G1.south west)+(-0.3, -0.1)$) ($(n1.north east)+(0.0, 0.1)$)}, fill=black!20!white, draw, dashed, inner sep=0pt] (sensor1) {}; \node[below right] at (sensor1.north west) {Sensor 1}; \node[fit={($(G2.south west)+(-0.3, -0.1)$) ($(n2.north east)+(0.0, 0.1)$)}, fill=black!20!white, draw, dashed, inner sep=0pt] (sensor2) {}; \node[below right] at (sensor2.north west) {Sensor 2}; \end{scope} \end{tikzpicture}