ESRF Double Crystal Monochromator - Feedback Controller
Table of Contents
This report is also available as a pdf.
1. Estimation of Sensitivity Function
1.1. Load Data
Two scans are performed:
1.1in mode B3.1in mode C
The difference between the two is that mode C adds the feedback controller.
%% Load Data of the new LUT method Ts = 0.1; ol_drx = 1e-9*double(h5read('xanes_0003.h5','/1.1/measurement/xtal_111_drx_filter')); % Rx [rad] cl_drx = 1e-9*double(h5read('xanes_0003.h5','/3.1/measurement/xtal_111_drx_filter')); % Rx [rad] ol_dry = 1e-9*double(h5read('xanes_0003.h5','/1.1/measurement/xtal_111_dry_filter')); % Ry [rad] cl_dry = 1e-9*double(h5read('xanes_0003.h5','/3.1/measurement/xtal_111_dry_filter')); % Ry [rad] t = linspace(Ts, Ts*length(ol_drx), length(ol_drx));
By comparison the frequency content of the crystal orientation errors between mode B and mode C, it is possible to estimate the Sensitivity transfer function (Figure 1).
win = hanning(ceil(1/Ts)); [pxx_ol_drx, f] = pwelch(ol_drx, win, [], [], 1/Ts); [pxx_cl_drx, ~] = pwelch(cl_drx, win, [], [], 1/Ts); [pxx_ol_dry, ~] = pwelch(ol_dry, win, [], [], 1/Ts); [pxx_cl_dry, ~] = pwelch(cl_dry, win, [], [], 1/Ts);
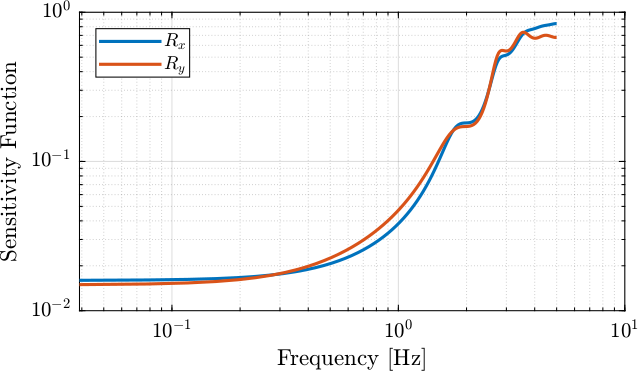
Figure 1: Estimation of the sensitivity transfer function magnitude
1.2. Controller
load('X_tal_cage_PID.mat', 'K');
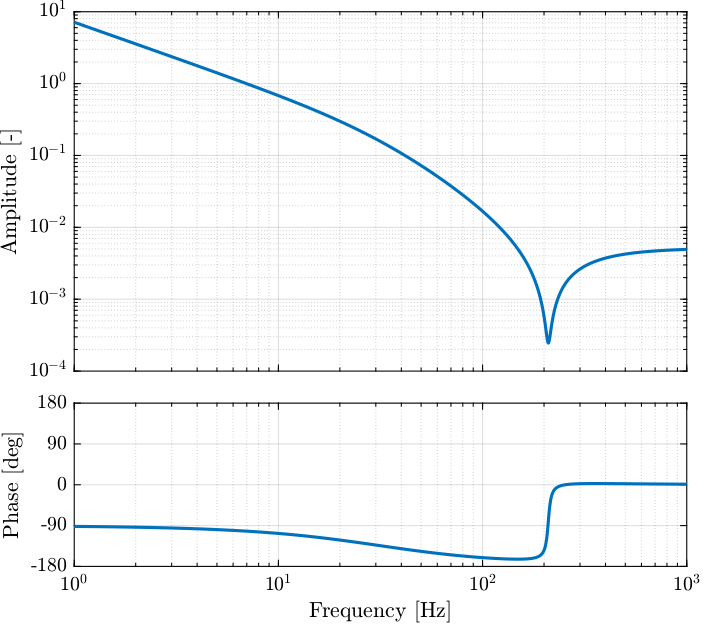
Figure 2: Bode Plot of the Controller
1.3. Test
Ts = 5e-3; cl_drx = 1e-9*double(h5read('xanes_0003.h5','/16.1/measurement/xtal_111_drx_filter')); % Rx [rad] ol_drx = 1e-9*double(h5read('xanes_0003.h5','/18.1/measurement/xtal_111_drx_filter')); % Rx [rad] t = linspace(Ts, Ts*length(ol_drx), length(ol_drx));
figure; hold on; plot(t, ol_drx) plot(t, cl_drx)
win = hanning(ceil(10/Ts)); [pxx_ol_drx, f] = pwelch(ol_drx, win, [], [], 1/Ts); [pxx_cl_drx, ~] = pwelch(cl_drx, win, [], [], 1/Ts);
2. System Identification
2.1. Identification
ur = load('FJPUR_step.mat'); uh = load('FJPUH_step.mat'); d = load('FJPD_step.mat');
| 1 | dz311 |
| 2 | dry311 |
| 3 | drx311 |
| 4 | dz111 |
| 5 | dry111 |
| 6 | drx111 |
| 7 | fjpur |
| 8 | fjpuh |
| 9 | fjpd |
| 10 | bragg |
ur.time = ur.time - ur.time(1); ur.allValues(:, 1) = ur.allValues(:, 1) - mean(ur.allValues(ur.time<1, 1)); ur.allValues(:, 2) = ur.allValues(:, 2) - mean(ur.allValues(ur.time<1, 2)); ur.allValues(:, 3) = ur.allValues(:, 3) - mean(ur.allValues(ur.time<1, 3)); t_filt = ur.time > 48 & ur.time < 60; ur.u = ur.allValues(t_filt, 7); ur.y_111 = [-ur.allValues(t_filt, 1), ur.allValues(t_filt, 2), ur.allValues(t_filt, 3)];
uh.time = uh.time - uh.time(1); uh.allValues(:, 1) = uh.allValues(:, 1) - mean(uh.allValues(uh.time<1, 1)); uh.allValues(:, 2) = uh.allValues(:, 2) - mean(uh.allValues(uh.time<1, 2)); uh.allValues(:, 3) = uh.allValues(:, 3) - mean(uh.allValues(uh.time<1, 3)); uh.u = uh.allValues(t_filt, 8); uh.y_111 = [-uh.allValues(t_filt, 1), uh.allValues(t_filt, 2), uh.allValues(t_filt, 3)];
d.time = d.time - d.time(1); d.allValues(:, 1) = d.allValues(:, 1) - mean(d.allValues(d.time<1, 1)); d.allValues(:, 2) = d.allValues(:, 2) - mean(d.allValues(d.time<1, 2)); d.allValues(:, 3) = d.allValues(:, 3) - mean(d.allValues(d.time<1, 3)); d.u = d.allValues(t_filt, 9); d.y_111 = [-d.allValues(t_filt, 1), d.allValues(t_filt, 2), d.allValues(t_filt, 3)];
J_a_111 = [1, 0.14, -0.0675 1, 0.14, 0.1525 1, -0.14, 0.0425]; J_a_311 = [1, 0.14, -0.1525 1, 0.14, 0.0675 1, -0.14, -0.0425]; ur.y = [J_a_311 * ur.y_111']'; uh.y = [J_a_311 * uh.y_111']'; d.y = [J_a_311 * d.y_111']';
%% Sampling Time and Frequency Ts = 1e-4; % [s] Fs = 1/Ts; % [Hz] % Hannning Windows win = hanning(ceil(5*Fs));
%% And we get the frequency vector [G_ur, f] = tfestimate(ur.u, ur.y, win, [], [], 1/Ts); [G_uh, ~] = tfestimate(uh.u, uh.y, win, [], [], 1/Ts); [G_d, ~] = tfestimate(d.u, d.y, win, [], [], 1/Ts);
[coh_ur, ~] = mscohere(ur.u, ur.y, win, [], [], 1/Ts); [coh_uh, ~] = mscohere(uh.u, uh.y, win, [], [], 1/Ts); [coh_d, ~] = mscohere(d.u, d.y, win, [], [], 1/Ts);
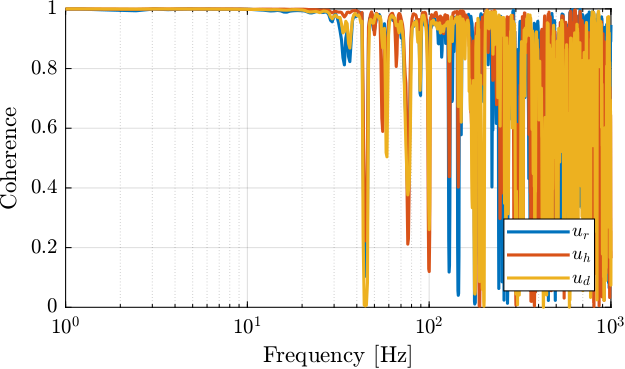
Figure 3: Coherence
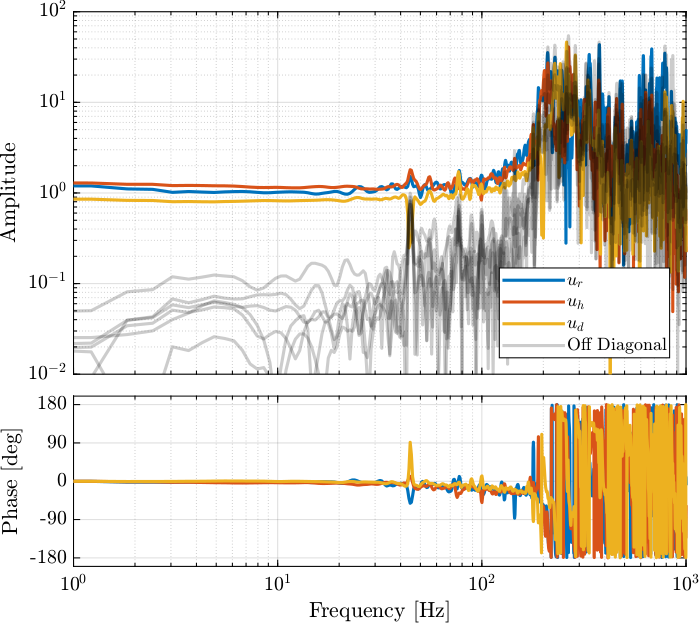
Figure 4: Bode Plot of the DCM dynamics in the frame of the fast jack.
%% Previously used controller load('X_tal_cage_PID.mat', 'K');
%% Controller design s = tf('s'); % Lead a = 4; % Amount of phase lead / width of the phase lead / high frequency gain wc = 2*pi*20; % Frequency with the maximum phase lead [rad/s] % Low Pass Filter w0 = 2*pi*100; % Cut-off frequency [rad/s] xi = 0.4; % Damping Ratio Kb = eye(3)*(2*pi*20)^2/(s^2) *1/(sqrt(a))* (1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a))) * 1/(1 + 2*xi/w0*s + s^2/w0^2);;
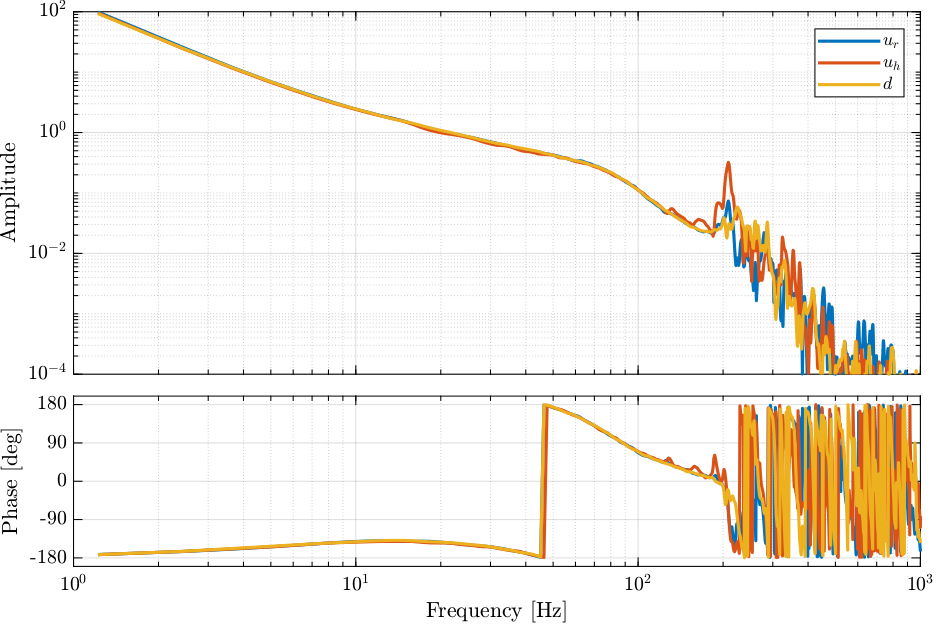
Figure 5: Loop gain
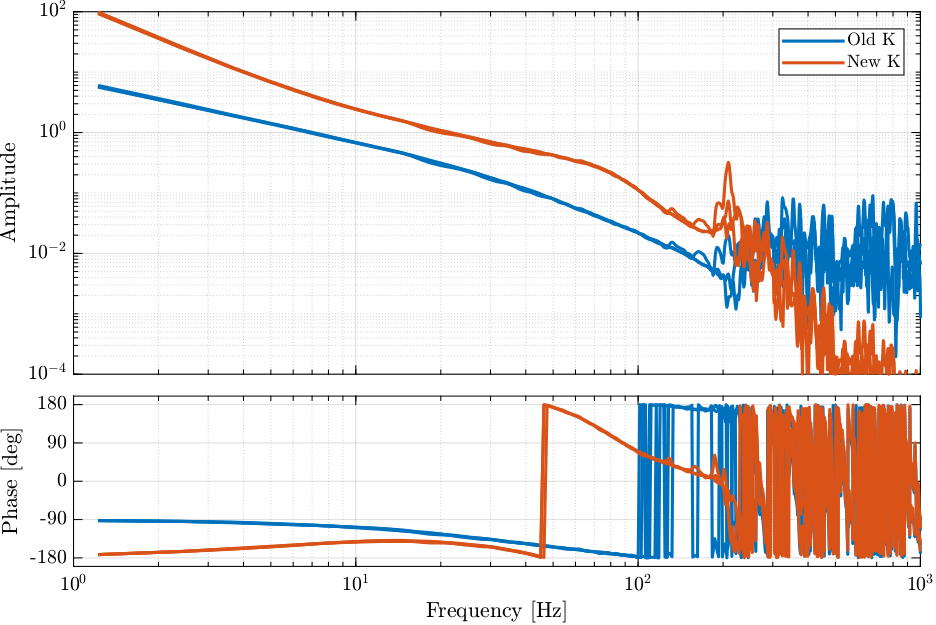
Figure 6: Loop gain
Compare Sensitivity functions
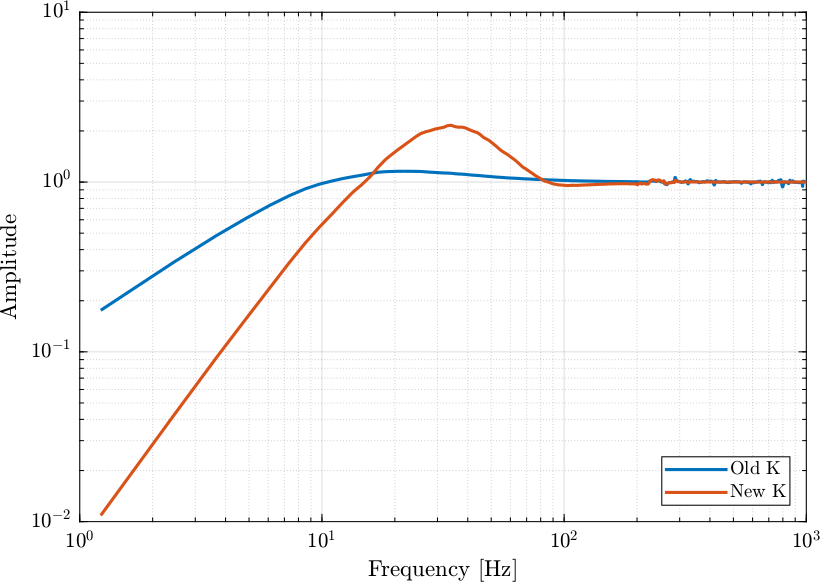
Figure 7: Comparison of sensitivity functions
L = zeros(3, 3, length(f)); Lb = zeros(3, 3, length(f)); for i_f = 1:length(f) L(:,:,i_f) = [G_ur(i_f,:); G_uh(i_f,:); G_d(i_f,:)]*freqresp(K , f(i_f), 'Hz'); Lb(:,:,i_f) = [G_ur(i_f,:); G_uh(i_f,:); G_d(i_f,:)]*freqresp(Kb, f(i_f), 'Hz'); end
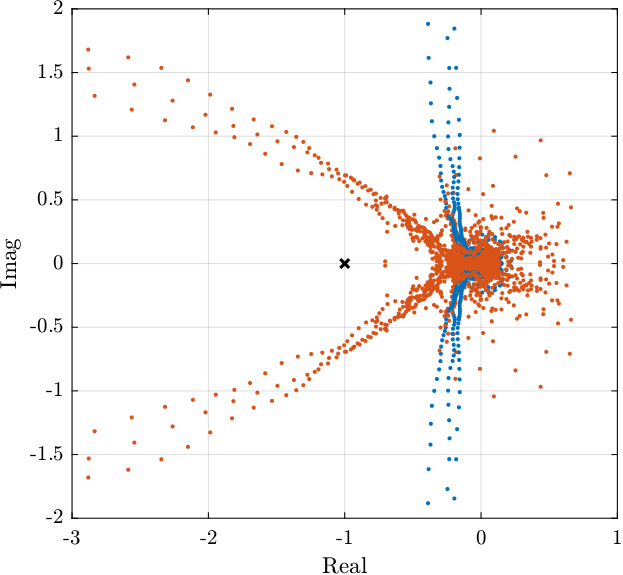
Figure 8: Root Locus
2.2. Identification - New
ur = load('FJPUR_step_new.mat'); uh = load('FJPUH_step_new.mat'); d = load('FJPD_step_new.mat');
| 1 | dz311 |
| 2 | dry311 |
| 3 | drx311 |
| 4 | dz111 |
| 5 | dry111 |
| 6 | drx111 |
| 7 | fjpur |
| 8 | fjpuh |
| 9 | fjpd |
| 10 | bragg |
ur.time = ur.time - ur.time(1); ur.allValues(:, 1) = ur.allValues(:, 1) - mean(ur.allValues(ur.time<0.1, 1)); ur.allValues(:, 2) = ur.allValues(:, 2) - mean(ur.allValues(ur.time<0.1, 2)); ur.allValues(:, 3) = ur.allValues(:, 3) - mean(ur.allValues(ur.time<0.1, 3)); t_filt = ur.time < 5; ur.u = ur.allValues(t_filt, 7); ur.y_111 = [-ur.allValues(t_filt, 1), ur.allValues(t_filt, 2), ur.allValues(t_filt, 3)];
uh.time = uh.time - uh.time(1); uh.allValues(:, 1) = uh.allValues(:, 1) - mean(uh.allValues(uh.time<0.1, 1)); uh.allValues(:, 2) = uh.allValues(:, 2) - mean(uh.allValues(uh.time<0.1, 2)); uh.allValues(:, 3) = uh.allValues(:, 3) - mean(uh.allValues(uh.time<0.1, 3)); uh.u = uh.allValues(t_filt, 8); uh.y_111 = [-uh.allValues(t_filt, 1), uh.allValues(t_filt, 2), uh.allValues(t_filt, 3)];
d.time = d.time - d.time(1); d.allValues(:, 1) = d.allValues(:, 1) - mean(d.allValues(d.time<0.1, 1)); d.allValues(:, 2) = d.allValues(:, 2) - mean(d.allValues(d.time<0.1, 2)); d.allValues(:, 3) = d.allValues(:, 3) - mean(d.allValues(d.time<0.1, 3)); d.u = d.allValues(t_filt, 9); d.y_111 = [-d.allValues(t_filt, 1), d.allValues(t_filt, 2), d.allValues(t_filt, 3)];
J_a_111 = [1, 0.14, -0.0675 1, 0.14, 0.1525 1, -0.14, 0.0425]; J_a_311 = [1, 0.14, -0.1525 1, 0.14, 0.0675 1, -0.14, -0.0425]; ur.y = [J_a_311 * ur.y_111']'; uh.y = [J_a_311 * uh.y_111']'; d.y = [J_a_311 * d.y_111']';
%% Sampling Time and Frequency Ts = 1e-4; % [s] Fs = 1/Ts; % [Hz] % Hannning Windows win = hanning(ceil(5*Fs));
%% And we get the frequency vector [G_ur, f] = tfestimate(ur.u, ur.y, win, [], [], 1/Ts); [G_uh, ~] = tfestimate(uh.u, uh.y, win, [], [], 1/Ts); [G_d, ~] = tfestimate(d.u, d.y, win, [], [], 1/Ts);
[coh_ur, ~] = mscohere(ur.u, ur.y, win, [], [], 1/Ts); [coh_uh, ~] = mscohere(uh.u, uh.y, win, [], [], 1/Ts); [coh_d, ~] = mscohere(d.u, d.y, win, [], [], 1/Ts);
%% Previously used controller load('X_tal_cage_PID.mat', 'K');
%% Controller design s = tf('s'); % Lead a = 4; % Amount of phase lead / width of the phase lead / high frequency gain wc = 2*pi*20; % Frequency with the maximum phase lead [rad/s] % Low Pass Filter w0 = 2*pi*100; % Cut-off frequency [rad/s] xi = 0.4; % Damping Ratio Kb = eye(3)*(2*pi*20)^2/(s^2) *1/(sqrt(a))* (1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a))) * 1/(1 + 2*xi/w0*s + s^2/w0^2);;
Compare Sensitivity functions

Figure 9: Comparison of sensitivity functions
L = zeros(3, 3, length(f)); Lb = zeros(3, 3, length(f)); for i_f = 1:length(f) L(:,:,i_f) = [G_ur(i_f,:); G_uh(i_f,:); G_d(i_f,:)]*freqresp(K , f(i_f), 'Hz'); Lb(:,:,i_f) = [G_ur(i_f,:); G_uh(i_f,:); G_d(i_f,:)]*freqresp(Kb, f(i_f), 'Hz'); end

Figure 10: Root Locus
2.3. Identification - White noise
ur = load('fjpur_white_noise.mat'); uh = load('fjpuh_white_noise.mat'); d = load('fjpd_white_noise.mat');
| 1 | dz111 |
| 2 | dry111 |
| 3 | drx111 |
| 4 | fjpur |
| 5 | fjpuh |
| 6 | fjpd |
| 7 | bragg |
ur.time = ur.time - ur.time(1); ur.drx = ur.drx - mean(ur.drx); ur.dry = ur.dry - mean(ur.dry); ur.dz = ur.dz - mean(ur.dz);
uh.time = uh.time - uh.time(1); uh.drx = uh.drx - mean(uh.drx); uh.dry = uh.dry - mean(uh.dry); uh.dz = uh.dz - mean(uh.dz);
d.time = d.time - d.time(1); d.drx = d.drx - mean(d.drx); d.dry = d.dry - mean(d.dry); d.dz = d.dz - mean(d.dz);
J_a_111 = [1, 0.14, -0.0675 1, 0.14, 0.1525 1, -0.14, 0.0425]; ur.y = [J_a_111 * [-ur.dz, ur.dry, ur.drx]']'; uh.y = [J_a_111 * [-uh.dz, uh.dry, uh.drx]']'; d.y = [J_a_111 * [-d.dz, d.dry, d.drx]']';
%% Sampling Time and Frequency Ts = 1e-4; % [s] Fs = 1/Ts; % [Hz] % Hannning Windows win = hanning(ceil(0.5*Fs));
%% And we get the frequency vector [G_ur, f] = tfestimate(ur.fjpur, ur.y, win, [], [], 1/Ts); [G_uh, ~] = tfestimate(uh.fjpuh, uh.y, win, [], [], 1/Ts); [G_d, ~] = tfestimate(d.fjpd, d.y, win, [], [], 1/Ts);
[coh_ur, ~] = mscohere(ur.fjpur, ur.y, win, [], [], 1/Ts); [coh_uh, ~] = mscohere(uh.fjpuh, uh.y, win, [], [], 1/Ts); [coh_d, ~] = mscohere(d.fjpd, d.y, win, [], [], 1/Ts);
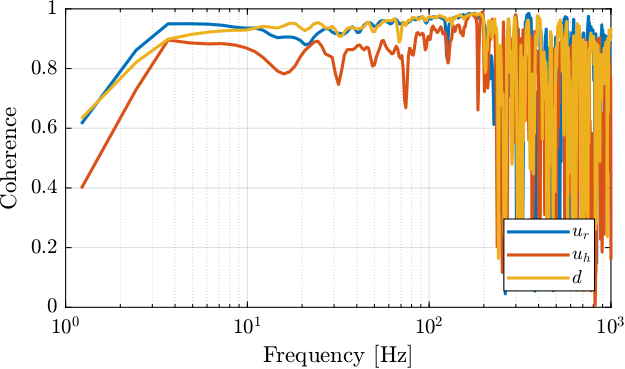
Figure 11: description
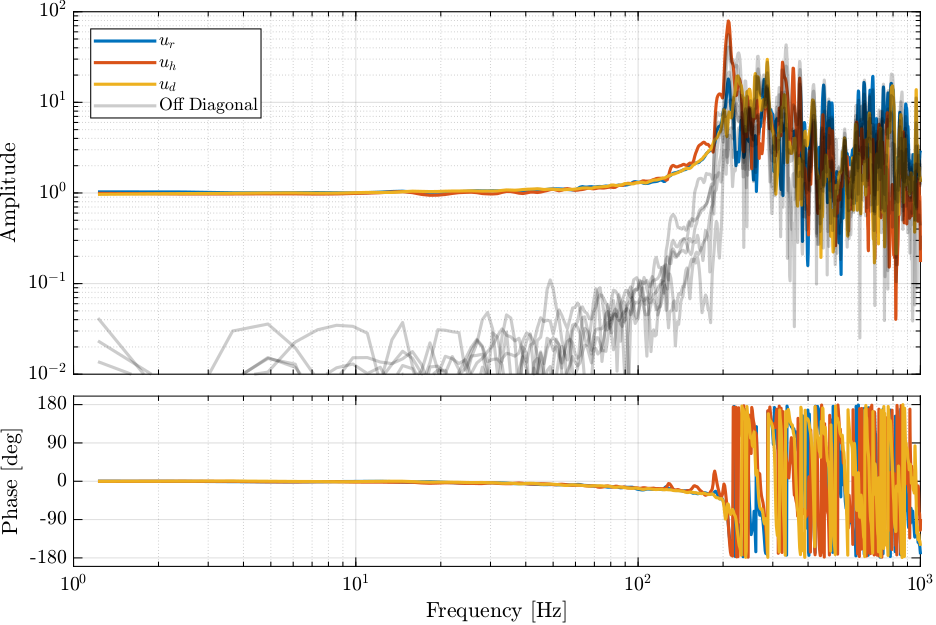
Figure 12: Bode Plot of the DCM dynamics in the frame of the fast jack.
%% Previously used controller load('X_tal_cage_PID.mat', 'K');
%% Controller design s = tf('s'); % Lead a = 8; % Amount of phase lead / width of the phase lead / high frequency gain wc = 2*pi*20; % Frequency with the maximum phase lead [rad/s] % Low Pass Filter w0 = 2*pi*80; % Cut-off frequency [rad/s] xi = 0.4; % Damping Ratio Kb = eye(3)*(2*pi*20)^2/(s^2) *1/(sqrt(a))* (1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a))) * 1/(1 + 2*xi/w0*s + s^2/w0^2);;

Figure 13: Loop gain

Figure 14: Loop gain
Compare Sensitivity functions

Figure 15: Comparison of sensitivity functions
L = zeros(3, 3, length(f)); Lb = zeros(3, 3, length(f)); for i_f = 1:length(f) L(:,:,i_f) = [G_ur(i_f,:); G_uh(i_f,:); G_d(i_f,:)]*freqresp(K , f(i_f), 'Hz'); Lb(:,:,i_f) = [G_ur(i_f,:); G_uh(i_f,:); G_d(i_f,:)]*freqresp(Kb, f(i_f), 'Hz'); end

Figure 16: Root Locus
2.4. Test
%% Notch gm = 0.015; xi = 0.1; wn = 2*pi*208; K_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);
%% Double integrator w0 = 2*pi*40; K_int = (w0^2)/(s^2);
%% Lead a = 3; % Amount of phase lead / width of the phase lead / high frequency gain K_lead = 1/(sqrt(a))*(1 + s/(w0/sqrt(a)))/(1 + s/(w0*sqrt(a))); K_lead = K_lead*K_lead;
%% Low Pass Filter w0 = 2*pi*120; % Cut-off frequency [rad/s] xi = 0.3; % Damping Ratio K_lpf = 1/(1 + 2*xi/w0*s + s^2/w0^2);
%% Diagonal controller Kb = 0.8*eye(3)*K_notch*K_int*K_lead*K_lpf;
2.5. New controller - Higher bandwidth
%% Previously used controller load('X_tal_cage_PID.mat', 'K');
%% Current Controller design % Lead a = 8; % Amount of phase lead / width of the phase lead / high frequency gain wc = 2*pi*20; % Frequency with the maximum phase lead [rad/s] % Low Pass Filter w0 = 2*pi*80; % Cut-off frequency [rad/s] xi = 0.4; % Damping Ratio Kb_old = eye(3)*(2*pi*20)^2/(s^2) *1/(sqrt(a))* (1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a))) * 1/(1 + 2*xi/w0*s + s^2/w0^2);;
%% Notch gm = 0.015; xi = 0.2; wn = 2*pi*208; K_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);
%% Double integrator w0 = 2*pi*40; K_int = (w0^2)/(s^2);
%% Lead a = 3; % Amount of phase lead / width of the phase lead / high frequency gain w0 = 2*pi*40; K_lead = 1/(sqrt(a))*(1 + s/(w0/sqrt(a)))/(1 + s/(w0*sqrt(a))); K_lead = K_lead*K_lead;
%% Low Pass Filter w0 = 2*pi*120; % Cut-off frequency [rad/s] xi = 0.3; % Damping Ratio K_lpf = 1/(1 + 2*xi/w0*s + s^2/w0^2);
%% Diagonal controller Kb = 0.9*eye(3)*K_notch*K_int*K_lead*K_lpf;
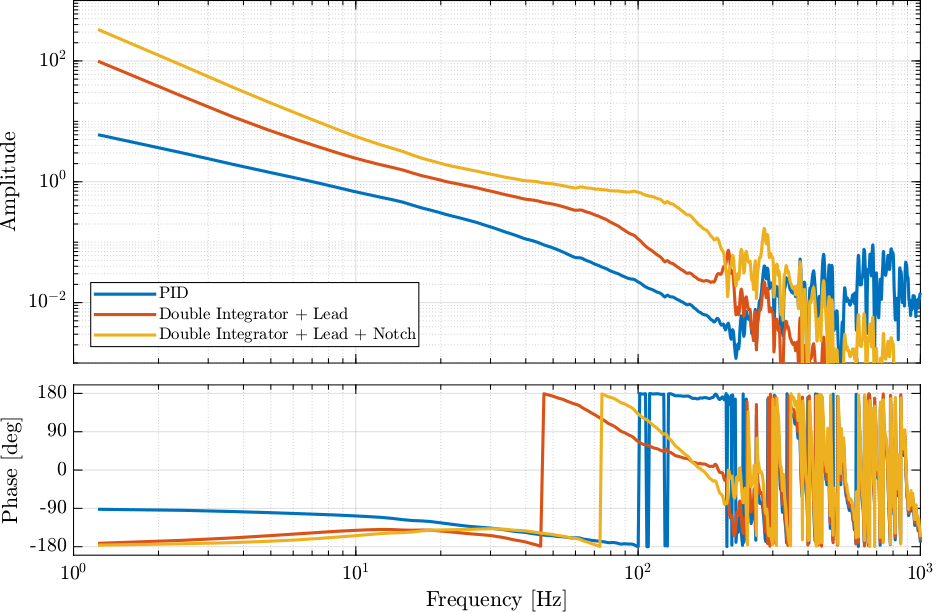
Figure 17: description
L = zeros(3, 3, length(f)); Lb = zeros(3, 3, length(f)); Lb_new = zeros(3, 3, length(f)); for i_f = 1:length(f) L(:,:,i_f) = [G_ur(i_f,:); G_uh(i_f,:); G_d(i_f,:)]*freqresp(K , f(i_f), 'Hz'); Lb(:,:,i_f) = [G_ur(i_f,:); G_uh(i_f,:); G_d(i_f,:)]*freqresp(Kb_old, f(i_f), 'Hz'); Lb_new(:,:,i_f) = [G_ur(i_f,:); G_uh(i_f,:); G_d(i_f,:)]*freqresp(Kb, f(i_f), 'Hz'); end
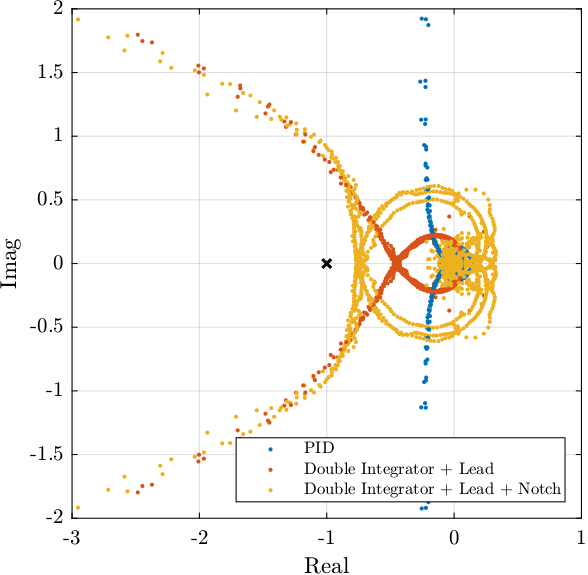
Figure 18: n
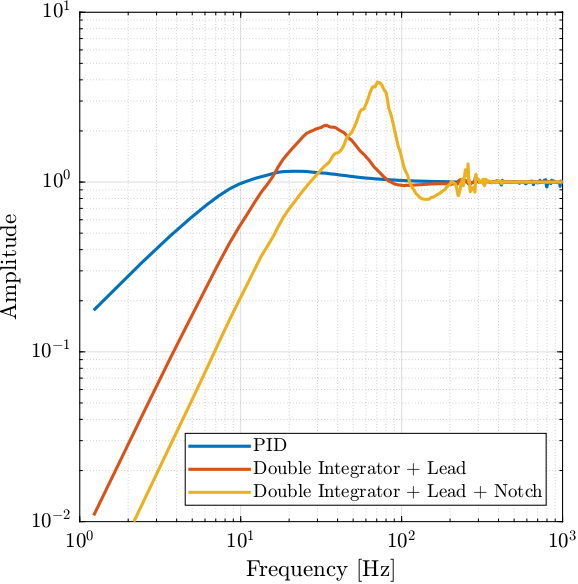
Figure 19: description
2.6. Added gain
%% Notch gm = 0.015; xi = 0.2; wn = 2*pi*208; K_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);
%% Double integrator w0 = 2*pi*40; K_int = (w0^2)/(s^2);
%% Lead a = 3; % Amount of phase lead / width of the phase lead / high frequency gain w0 = 2*pi*40; K_lead = 1/(sqrt(a))*(1 + s/(w0/sqrt(a)))/(1 + s/(w0*sqrt(a))); K_lead = K_lead*K_lead;
%% Low Pass Filter w0 = 2*pi*120; % Cut-off frequency [rad/s] xi = 0.3; % Damping Ratio K_lpf = 1/(1 + 2*xi/w0*s + s^2/w0^2);
gm = 10; xi = 0.02; wn = 2*pi*15; H = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);
%% Diagonal controller Kb_gain = 0.9*eye(3)*H*K_notch*K_int*K_lead*K_lpf;
Lb_gain = zeros(3, 3, length(f)); for i_f = 1:length(f) Lb_gain(:,:,i_f) = [G_ur(i_f,:); G_uh(i_f,:); G_d(i_f,:)]*freqresp(Kb_gain, f(i_f), 'Hz'); end
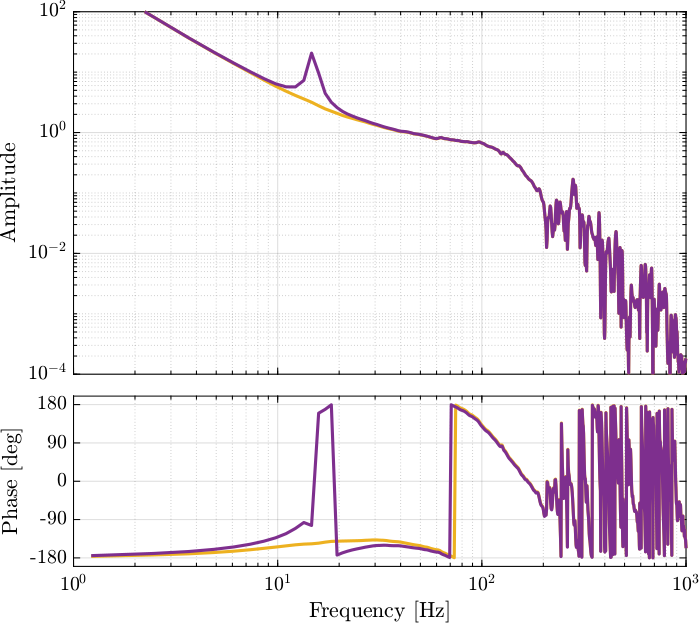
Figure 20: description
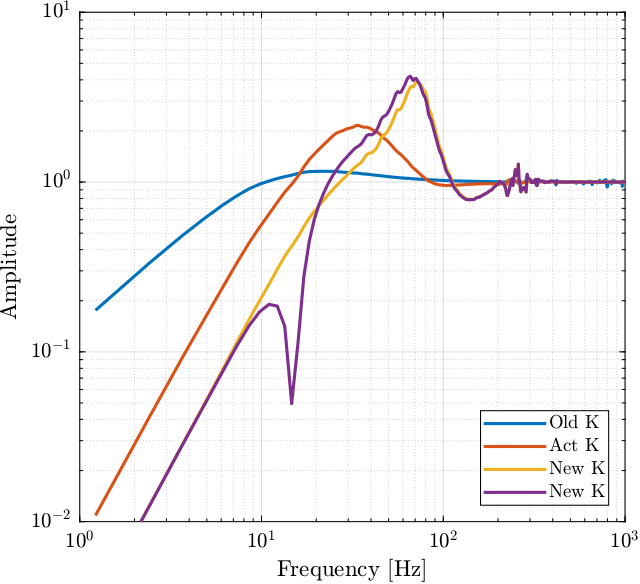
Figure 21: description
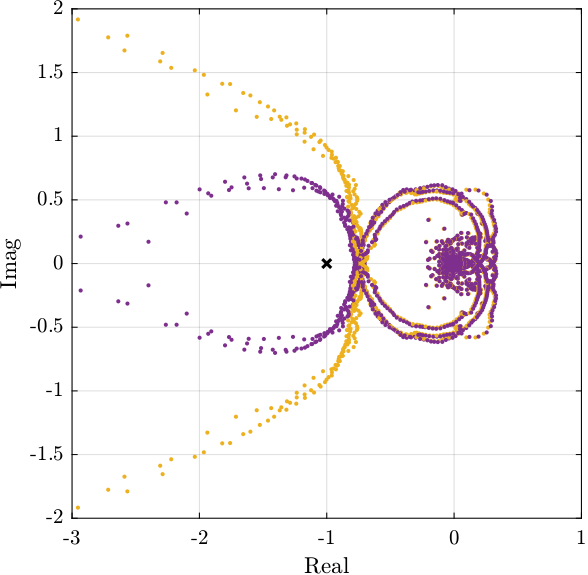
Figure 22: nyquist plot
3. Noise Budgeting
3.1. No Displacement
| 1 | dz311 |
| 2 | dry311 |
| 3 | drx311 |
| 4 | dz111 |
| 5 | dry111 |
| 6 | drx111 |
| 7 | fjpur |
| 8 | fjpuh |
| 9 | fjpd |
| 10 | bragg |
data_10_deg = load('no_mov_10.mat'); data_70_deg = load('no_mov_70.mat');
data_10_deg = extractDatData('no_mov_10.mat', ... {"dz311", "dry311", "drx311", "dz", "dry", "drx", "fjpur", "fjpuh", "fjpd", "bragg"}, ... [1e-9, 1e-9, 1e-9, 1e-9, 1e-9, 1e-9, 1e-8, 1e-8, 1e-8, pi/180]); data_10_deg = processMeasData(data_10_deg);
Ts = 1e-4; t = Ts*[1:length(data_10_deg.bragg)];
data_10_deg.dz = data_10_deg.allValues(:,4) - mean(data_10_deg.allValues(:,4)); data_10_deg.dry = data_10_deg.allValues(:,5) - mean(data_10_deg.allValues(:,5)); data_10_deg.drx = data_10_deg.allValues(:,6) - mean(data_10_deg.allValues(:,6));
%% Compute motion error in the frame of the fast jack J_a_111 = [1, 0.14, -0.1525 1, 0.14, 0.0675 1, -0.14, 0.0425]; de_111 = [data_10_deg.dz'; data_10_deg.dry'; data_10_deg.drx']; de_fj = J_a_111*de_111; data_10_deg.fj_ur = de_fj(1,:)'; data_10_deg.fj_uh = de_fj(2,:)'; data_10_deg.fj_d = de_fj(3,:)'; de_111 = [data_70_deg.dz'; data_70_deg.dry'; data_70_deg.drx']; de_fj = J_a_111*de_111; data_70_deg.fj_ur = de_fj(1,:)'; data_70_deg.fj_uh = de_fj(2,:)'; data_70_deg.fj_d = de_fj(3,:)';
win = hanning(ceil(1/Ts)); [pxx_10_ur, f] = pwelch(data_10_deg.fj_ur, win, [], [], 1/Ts); [pxx_70_ur, ~] = pwelch(data_70_deg.fj_ur, win, [], [], 1/Ts); [pxx_10_uh, ~] = pwelch(data_10_deg.fj_uh, win, [], [], 1/Ts); [pxx_70_uh, ~] = pwelch(data_70_deg.fj_uh, win, [], [], 1/Ts); [pxx_10_d, ~] = pwelch(data_10_deg.fj_d, win, [], [], 1/Ts); [pxx_70_d, ~] = pwelch(data_70_deg.fj_d, win, [], [], 1/Ts);
CPS_10_ur = flip(-cumtrapz(flip(f), flip(pxx_10_ur))); CPS_10_uh = flip(-cumtrapz(flip(f), flip(pxx_10_uh))); CPS_10_d = flip(-cumtrapz(flip(f), flip(pxx_10_d))); CPS_70_ur = flip(-cumtrapz(flip(f), flip(pxx_70_ur))); CPS_70_uh = flip(-cumtrapz(flip(f), flip(pxx_70_uh))); CPS_70_d = flip(-cumtrapz(flip(f), flip(pxx_70_d)));
figure; hold on; plot(f, sqrt(CPS_10_ur), '-' , 'color', colors(1, :), 'DisplayName', '10 deg - $u_r$') plot(f, sqrt(CPS_70_ur), '--', 'color', colors(1, :), 'DisplayName', '70 deg - $u_r$') plot(f, sqrt(CPS_10_uh), '-' , 'color', colors(2, :), 'DisplayName', '10 deg - $u_h$') plot(f, sqrt(CPS_70_uh), '--', 'color', colors(2, :), 'DisplayName', '70 deg - $u_h$') plot(f, sqrt(CPS_10_d), '-' , 'color', colors(3, :), 'DisplayName', '10 deg - $d$') plot(f, sqrt(CPS_70_d), '--', 'color', colors(3, :), 'DisplayName', '70 deg - $d$') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); xlabel('Frequency [Hz]'); ylabel('ASD [$\frac{nrad}{\sqrt{Hz}}$]'); legend('location', 'northwest'); xlim([1, 1e3]);
figure; hold on; plot(f, sqrt(pxx_10_ur)) plot(f, sqrt(pxx_70_ur)) hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); xlabel('Frequency [Hz]'); ylabel('ASD [$\frac{nrad}{\sqrt{Hz}}$]'); legend('location', 'northwest'); xlim([1, 1e3]);
data_70_deg.dz = data_70_deg.allValues(:,4) - mean(data_70_deg.allValues(:,4)); data_70_deg.dry = data_70_deg.allValues(:,5) - mean(data_70_deg.allValues(:,5)); data_70_deg.drx = data_70_deg.allValues(:,6) - mean(data_70_deg.allValues(:,6));
win = hanning(ceil(1/Ts)); [pxx_10_drx, f] = pwelch(data_10_deg.drx, win, [], [], 1/Ts); [pxx_70_drx, ~] = pwelch(data_70_deg.drx, win, [], [], 1/Ts); [pxx_10_dry, ~] = pwelch(data_10_deg.dry, win, [], [], 1/Ts); [pxx_70_dry, ~] = pwelch(data_70_deg.dry, win, [], [], 1/Ts); [pxx_10_dz, ~] = pwelch(data_10_deg.dz, win, [], [], 1/Ts); [pxx_70_dz, ~] = pwelch(data_70_deg.dz, win, [], [], 1/Ts);
figure; hold on; plot(f, sqrt(pxx_10_drx)) plot(f, sqrt(pxx_70_drx)) hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); xlabel('Frequency [Hz]'); ylabel('ASD [$\frac{nrad}{\sqrt{Hz}}$]'); legend('location', 'northwest'); xlim([1, 1e3]);
figure; hold on; plot(f, sqrt(pxx_10_dry)) plot(f, sqrt(pxx_70_dry)) hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); xlabel('Frequency [Hz]'); ylabel('ASD [$\frac{nrad}{\sqrt{Hz}}$]'); legend('location', 'northwest'); xlim([1, 1e3]);
figure; hold on; plot(f, sqrt(pxx_10_dz)) plot(f, sqrt(pxx_70_dz)) hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); xlabel('Frequency [Hz]'); ylabel('ASD [$\frac{nm}{\sqrt{Hz}}$]'); legend('location', 'northwest'); xlim([1, 1e3]);
3.2. Scans
| 1 | dz311 |
| 2 | dry311 |
| 3 | drx311 |
| 4 | dz111 |
| 5 | dry111 |
| 6 | drx111 |
| 7 | fjpur |
| 8 | fjpuh |
| 9 | fjpd |
| 10 | bragg |
%% Load Data data_10_70_deg = extractDatData('thtraj_10_70.mat', ... {"dz311", "dry311", "drx311", "dz", "dry", "drx", "fjur", "fjuh", "fjd", "bragg"}, ... [1e-9, 1e-9, 1e-9, 1e-9, 1e-9, 1e-9, 1e-8, 1e-8, 1e-8, pi/180]); Ts = 1e-4; t = Ts*[1:length(data_10_70_deg.bragg)]; %% Actuator Jacobian J_a_111 = [1, 0.14, -0.0675 1, 0.14, 0.1525 1, -0.14, 0.0425]; data_10_70_deg.ddz = 10.5e-3./(2*cos(data_10_70_deg.bragg)) - data_10_70_deg.dz; %% Computation of the position of the FJ as measured by the interferometers error = J_a_111 * [data_10_70_deg.ddz, data_10_70_deg.dry, data_10_70_deg.drx]'; data_10_70_deg.fjur_e = error(1,:)'; % [m] data_10_70_deg.fjuh_e = error(2,:)'; % [m] data_10_70_deg.fjd_e = error(3,:)'; % [m]
%% Load Data data_70_10_deg = extractDatData('thtraj_70_10.mat', ... {"dz311", "dry311", "drx311", "dz", "dry", "drx", "fjur", "fjuh", "fjd", "bragg"}, ... [1e-9, 1e-9, 1e-9, 1e-9, 1e-9, 1e-9, 1e-8, 1e-8, 1e-8, pi/180]); %% Actuator Jacobian J_a_111 = [1, 0.14, -0.0675 1, 0.14, 0.1525 1, -0.14, 0.0425]; data_70_10_deg.ddz = 10.5e-3./(2*cos(data_70_10_deg.bragg)) - data_70_10_deg.dz; %% Computation of the position of the FJ as measured by the interferometers error = J_a_111 * [data_70_10_deg.ddz, data_70_10_deg.dry, data_70_10_deg.drx]'; data_70_10_deg.fjur_e = error(1,:)'; % [m] data_70_10_deg.fjuh_e = error(2,:)'; % [m] data_70_10_deg.fjd_e = error(3,:)'; % [m]
win = hanning(ceil(1/Ts)); [pxx_10_70_ur, f] = pwelch(data_10_70_deg.fjur_e(t<100), win, [], [], 1/Ts); [pxx_70_10_ur, ~] = pwelch(data_70_10_deg.fjur_e(t<100), win, [], [], 1/Ts); [pxx_10_70_uh, ~] = pwelch(data_10_70_deg.fjuh_e(t<100), win, [], [], 1/Ts); [pxx_70_10_uh, ~] = pwelch(data_70_10_deg.fjuh_e(t<100), win, [], [], 1/Ts); [pxx_10_70_d, ~] = pwelch(data_10_70_deg.fjd_e(t<100), win, [], [], 1/Ts); [pxx_70_10_d, ~] = pwelch(data_70_10_deg.fjd_e(t<100), win, [], [], 1/Ts);
CPS_10_70_ur = flip(-cumtrapz(flip(f), flip(pxx_10_70_ur))); CPS_10_70_uh = flip(-cumtrapz(flip(f), flip(pxx_10_70_uh))); CPS_10_70_d = flip(-cumtrapz(flip(f), flip(pxx_10_70_d))); CPS_70_10_ur = flip(-cumtrapz(flip(f), flip(pxx_70_10_ur))); CPS_70_10_uh = flip(-cumtrapz(flip(f), flip(pxx_70_10_uh))); CPS_70_10_d = flip(-cumtrapz(flip(f), flip(pxx_70_10_d)));
figure; hold on; plot(f, 1e9*sqrt(CPS_10_70_ur)) hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); xlabel('Frequency [Hz]'); ylabel('ASD [$\frac{nrad}{\sqrt{Hz}}$]'); legend('location', 'northwest'); xlim([1, 1e3]);
figure; hold on; plot(f, sqrt(pxx_10_70_ur)) plot(f, sqrt(pxx_70_10_ur)) hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); xlabel('Frequency [Hz]'); ylabel('ASD [$\frac{nrad}{\sqrt{Hz}}$]'); legend('location', 'northwest'); xlim([1, 1e3]);
3.3. Noise budgeting - No rotation
First, we look at the position errors when the bragg axis is not moving
%% Load Measurement Data ol_data = load('FJPUR_step.mat');
%% Pre-processing ol_time = ol_data.time - ol_data.time(1); ol_drx = ol_data.allValues(ol_time < 45, 6); ol_dry = ol_data.allValues(ol_time < 45, 5); ol_dz = ol_data.allValues(ol_time < 45, 4); ol_drx = ol_drx - mean(ol_drx); ol_dry = ol_dry - mean(ol_dry); ol_dz = ol_dz - mean(ol_dz); ol_time = ol_time(ol_time < 45);
figure; plot(ol_time, ol_drx)
%% Parameters for Spectral Analysis Ts = 1e-4; win = hanning(ceil(1/Ts));
%% Computation of the PSD [pxx_ol_drx, f] = pwelch(ol_drx, win, [], [], 1/Ts); [pxx_ol_dry, ~] = pwelch(ol_dry, win, [], [], 1/Ts); [pxx_ol_dz, ~] = pwelch(ol_dz, win, [], [], 1/Ts);
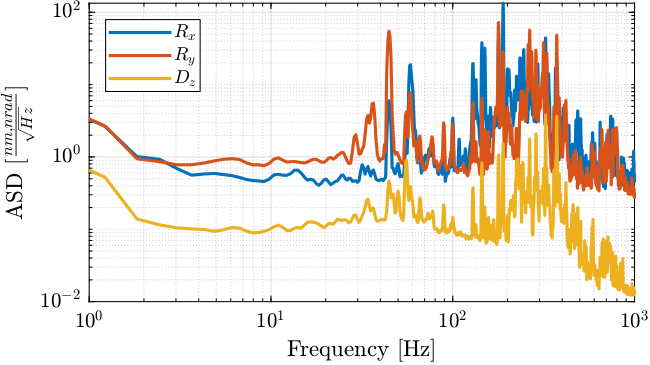
Figure 23: Amplitude Spectral Density
%% Cumulative Spectral Density CPS_drx = flip(-cumtrapz(flip(f), flip(pxx_ol_drx))); CPS_dry = flip(-cumtrapz(flip(f), flip(pxx_ol_dry))); CPS_dz = flip(-cumtrapz(flip(f), flip(pxx_ol_dz)));
%% Cumulative Spectral Density
CPS_drx = cumtrapz(f, pxx_ol_drx);
CPS_dry = cumtrapz(f, pxx_ol_dry);
CPS_dz = cumtrapz(f, pxx_ol_dz);
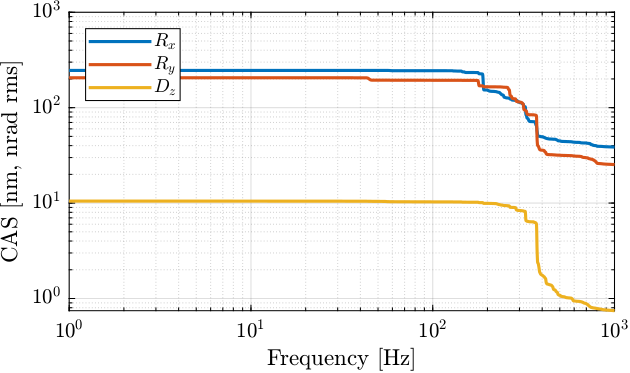
Figure 24: Cumulative Amplitude Spectrum
3.4. Noise budgeting - Bragg rotation
4. Test Mode C
4.1. Mode B and Mode C
data_B = extractDatData(sprintf("/home/thomas/mnt/data_id21/22Jan/blc13491/id21/test_regul_220119/%s","lut_const_fj_vel_19012022_1450.dat"), ... {"bragg", "dz", "dry", "drx", "fjur", "fjuh", "fjd"}, ... [pi/180, 1e-9, 1e-9, 1e-9, 1e-8, 1e-8, 1e-8]); data_B = processMeasData(data_B);
data_C = extractDatData(sprintf("/home/thomas/mnt/data_id21/22Jan/blc13491/id21/test_regul_220119/%s","lut_const_fj_vel_19012022_1454.dat"), ... {"bragg", "dz", "dry", "drx", "fjur", "fjuh", "fjd"}, ... [pi/180, 1e-9, 1e-9, 1e-9, 1e-8, 1e-8, 1e-8]); data_C = processMeasData(data_C);
figure; hold on; plot(180/pi*data_B.bragg, 1e9*data_B.drx) hold off; xlabel('Bragg Angle [deg]'); ylabel('DRX [nrad]');
figure; hold on; plot(180/pi*data_B.bragg, 1e9*data_B.fjur_e_filt) plot(180/pi*data_C.bragg, 1e9*data_C.fjur_e_filt) hold off; xlabel('Bragg Angle [deg]'); ylabel('FJUR Error [nm]');
figure; hold on; plot(180/pi*data_B.bragg, 1e9*data_B.fjur_e) plot(180/pi*data_C.bragg, 1e9*data_C.fjur_e) hold off; xlabel('Bragg Angle [deg]'); ylabel('FJUR Error [nm]');
%% FIR Filter Fs = 1e4; % Sampling Frequency [Hz] fir_order = 5000; % Filter's order delay = fir_order/2; % Delay induced by the filter B_fir = firls(5000, ... % Filter's order [0 5/(Fs/2) 10/(Fs/2) 1], ... % Frequencies [Hz] [1 1 0 0]); % Wanted Magnitudes
%% Filtering all measured Fast Jack Position using the FIR filter data_B.drx_filter = filter(B_fir, 1, data_B.drx); data_B.drx_filter(1:end-delay) = data_B.drx_filter(delay+1:end); data_C.drx_filter = filter(B_fir, 1, data_C.drx); data_C.drx_filter(1:end-delay) = data_C.drx_filter(delay+1:end);
figure; hold on; plot(180/pi*data_B.bragg, 1e9*data_B.drx_filter) plot(180/pi*data_C.bragg, 1e9*data_C.drx_filter) hold off; xlabel('Bragg Angle [deg]'); ylabel('DRX [nrad]');
Ts = 1e-4; win = hanning(ceil(1/Ts)); [pxx_B_drx, f] = pwelch(data_B.drx, win, [], [], 1/Ts); [pxx_C_drx, ~] = pwelch(data_C.drx, win, [], [], 1/Ts);
5. Export numerator and denominator
5.1. Export
K_order = 10;
load('X_tal_cage_PID.mat', 'K'); K_order = order(K(1,1)); Kz = c2d(K(1,1)*(1 + s/2/pi/2e3)^(9-K_order)/(1 + s/2/pi/2e3)^(9-K_order), 1e-4); [num, den] = tfdata(Kz, 'v'); formatSpec = '%.18e %.18e %.18e %.18e %.18e %.18e %.18e %.18e %.18e %.18e\n'; fileID = fopen('X_tal_cage_PID.dat', 'w'); fprintf(fileID, formatSpec, [num; den]'); fclose(fileID);
load('X_tal_cage_PID_20Hz.mat', 'K'); K_order = order(K(1,1)); Kz = c2d(K(1,1)*(1 + s/2/pi/2e3)^(9-K_order)/(1 + s/2/pi/2e3)^(9-K_order), 1e-4); [num, den] = tfdata(Kz, 'v'); formatSpec = '%.18e %.18e %.18e %.18e %.18e %.18e %.18e %.18e %.18e %.18e\n'; fileID = fopen('X_tal_cage_PID_20Hz.dat', 'w'); fprintf(fileID, formatSpec, [num; den]'); fclose(fileID);
load('X_tal_cage_PID_40Hz.mat', 'K'); K_order = order(K(1,1)); Kz = c2d(K(1,1)*(1 + s/2/pi/2e3)^(9-K_order)/(1 + s/2/pi/2e3)^(9-K_order), 1e-4); [num, den] = tfdata(Kz, 'v'); formatSpec = '%.18e %.18e %.18e %.18e %.18e %.18e %.18e %.18e %.18e %.18e\n'; fileID = fopen('X_tal_cage_PID_40Hz.dat', 'w'); fprintf(fileID, formatSpec, [num; den]'); fclose(fileID);
5.2. Verify
K_data = importdata('X_tal_cage_PID_20Hz.dat'); K = tf(K_data(1,:), K_data(2,:), 1e-4)